
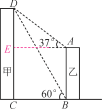
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.若乙比甲的水位高2cm时,注水时间m分钟,则m的值为( )

A.3或5B.4或6C.3或![]() D.5或9
D.5或9
查看答案和解析>>
科目:初中数学 来源: 题型:
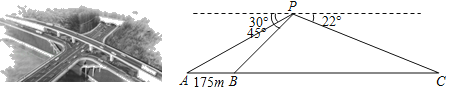
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道,它把六角亭老城区与知名景点女儿城连为一体,缓解了恩施城区交通拥堵的现状.如图,某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°,东端点B(隧道西进口)的俯角为45°,隧道东出口C的俯角为22°,已知黄石大桥AB全长175米,隧道BC的长约多少米(计算结果精确到1米)?(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=![]() 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() 且开口向下,则下列结论:①抛物线经过点
且开口向下,则下列结论:①抛物线经过点![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④对于任意实数
有两个不相等的实数根;④对于任意实数![]() ,
,![]() 总成立。其中结论正确的个数为( )
总成立。其中结论正确的个数为( )
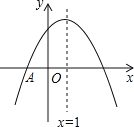
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
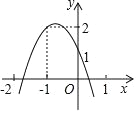
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<0;④b2+8a>4ac,其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
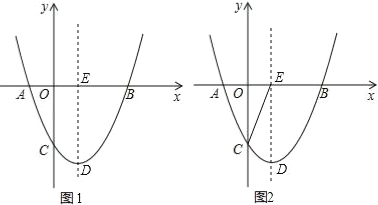
【题目】如图1,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),顶点为D,对称轴交x轴于点E.
(1)求该二次函数的解析式;
(2)设M为该抛物线对称轴左侧上的一点,过点M作直线MN∥x轴,交该抛物线于另一点N.是否存在点M,使四边形DMEN是菱形?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)连接CE(如图2),设点P是位于对称轴右侧该抛物线上一点,过点P作PQ⊥x轴,垂足为Q.连接PE,请求出当△PQE与△COE相似时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
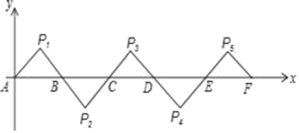
【题目】如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com