
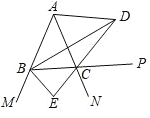
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
A.1 个B.2 个C.3 个D.4 个
【答案】D
【解析】
根据角平分线的定义、三角形的内角和定理、三角形的外角的性质、判断即可.
① ∵BD、CD分别平分△ABC的内角∠ABC、外角∠ACP,
∴∠ACP=2∠DCP,∠ABC=2∠DBC,
又∵∠ACP=∠BAC+∠ABC,∠DCP=∠DBC+∠BDC,
∴∠BAC=2∠BDE,
∴BDE ![]() BAC
BAC
∴①正确;
②∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC,
∴∠DBE=∠DBC+∠EBC=![]() ∠ABC+
∠ABC+![]() ∠MBC=
∠MBC=![]() ×180°=90°,
×180°=90°,
∴EB⊥DB,
故②正确,
③∵∠DCP=∠BDC+∠CBD,2∠DCP=∠BAC+2∠DBC,∴2(∠BDC+∠CBD)=∠BAC+2∠DBC,
∴∠BDC=![]() ∠BAC,
∠BAC,
∵∠BAC+2∠ACB=180°,
∴![]() ∠BAC+∠ACB=90°,
∠BAC+∠ACB=90°,
∴∠BDC+∠ACB=90°,
故③正确,
④∵∠BEC=180°![]() (∠MBC+∠NCB)
(∠MBC+∠NCB)
=180°![]() (∠BAC+∠ACB+∠BAC+∠ABC)
(∠BAC+∠ACB+∠BAC+∠ABC)
=180°![]() (180°+∠BAC)
(180°+∠BAC)
∴∠BEC=90°![]() ∠BAC,
∠BAC,
∴∠BAC+2∠BEC=180°,故④正确,
即正确的有4个,
故选D


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示数a、b,A、B之间的距离可表示为AB=|a﹣b|.已知数轴上A,B两点分别表示有理数﹣1和x.
(1)若AB=4时,则x的值为 ;
(2)当x=7时,点A,B分别以每秒1个单位长度和2个单位长度的速度同时向数轴负方向运动.求经过多少秒后,点A到原点的距离是点B到原点的距离的2倍;
(3)如图,点A,B,C,D四点在数轴上分别表示的数为﹣4,﹣1,2,6.是否存在点P在数轴上,使得点P到这四点的距离总和的最小?若存在,请直接写点P的位置和距离总和的最小值.若不存在,请说明理由;
![]()
(4)某一直线沿街有2020户民,假定相邻两户居民间隔相同,分别记为a1,a2,a3,a4,a5,…,a2020.某餐饮公司想为这2020户居民提供早餐,决定在路旁建立一个快餐店P.请问点P选在何处,才能使这2020户居民到点P的距离总和最小?试说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲公司单独做需要20天完成,乙公司单独做所用时间是甲公司的1.5倍.
(1)若甲、乙两公司合作完成这项工程需要多少天?
(2)若甲、乙两公司合作完成这项工程,在第10天结束时,甲公司有别的任务,不能继续合作,剩余部分由乙公司单独完成,则乙公司还需要做几天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() .
.

(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向
向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自点
自点![]() 向
向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,经过_________秒,
秒运动,经过_________秒,![]() 、
、![]() 两点相遇.
两点相遇.
(2)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,点
秒运动,点![]() 出发
出发![]() 秒后,点
秒后,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,问再经过几秒后
秒运动,问再经过几秒后![]() 、
、![]() 相距
相距![]() ?
?
(3)如图2:![]() ,
,![]() ,
,![]() ,点
,点![]() 绕着点
绕着点![]() 以
以![]() 度
度![]() 秒的速度逆时针旋转一周停止,同时点
秒的速度逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 、
、![]() 两点能相遇,直接写出点
两点能相遇,直接写出点![]() 运动的速度.
运动的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com