

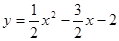 ;
;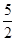 ,
,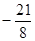 ),S△AME=
),S△AME=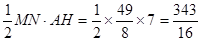
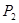 (
(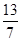 ,0)
,0)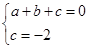 ∴
∴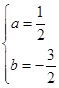
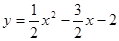
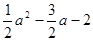
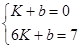 解得:
解得: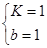 ∴y=x+1
∴y=x+1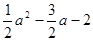 )= a+1-
)= a+1-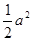 +
+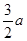 +2=-
+2=-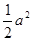 +
+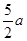 +3
+3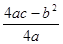 =
=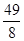 a=
a=
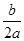 =
=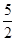
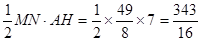 , M(
, M(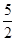 ,
,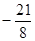 )
)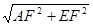 =
=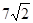
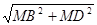 =
=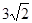
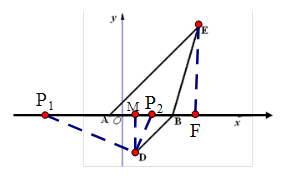
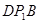 =∠AEB交X轴于点
=∠AEB交X轴于点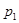
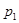
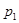 B=AB:BD
B=AB:BD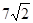 :
: 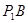 ="5:"
="5:" 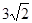
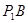 =
=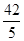
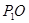 =
=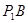 -OB=
-OB=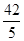 -4=
-4=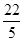
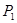 (-
(-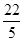 , 0)
, 0) 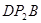 =∠ABE交X轴于点
=∠ABE交X轴于点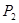
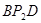
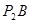 :AB
:AB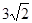 :
: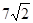 =
=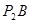 :5
:5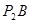 =
=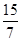
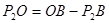 =4-
=4-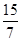 =
=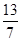
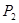 (
(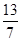 ,0)
,0)

科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

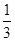 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式; ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (
( )与
)与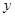 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点 ,
, ,点
,点 的坐标为(4,0).
的坐标为(4,0).
 是线段
是线段 上的动点,过点
上的动点,过点 作
作 ∥
∥ ,交
,交 于点
于点 ,连接
,连接 . 当
. 当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标; 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点 ,与直线
,与直线 交于点
交于点 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com