
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

【答案】(1)α;(2)△CPQ为等腰直角三角形.证明见解析.
【解析】
试题(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
试题解析:(1)证明:如图①,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE.在△ACD和△BCE中,
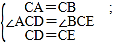
∴△ACD≌△BCE(SAS),
∴BE=AD.
(2)解:如图①,∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴∠AMB=180°-(180°-α)=α.
(3)解:△CPQ为等腰直角三角形.
证明:如图②,由(1)可得,BE=AD.
∵AD,BE的中点分别为点P,Q,
∴AP=BQ.
∵△ACD≌△BCE,
∴∠CAP=∠CBQ.在△ACP和△BCQ中,
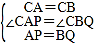
∴△ACP≌△BCQ(SAS),
∴CP=CQ且∠ACP=∠BCQ.
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
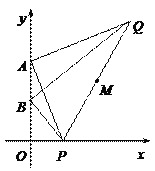
【题目】如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人做掷一个均匀小立方体的游戏,立方体的每个面上分别标有数字1,2,3,4,5,6,任意掷出小立方体后,若朝上的数字小于3,则甲获胜;若朝上的数字大于3 ,则乙获胜.你认为这个游戏对甲乙双方公平吗?为什么?你能不能就上面的小立方体设计一个较为公平的游戏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y轴上有一点A(0,1),点B是x轴上一点,∠ABO=60°,抛物线y=﹣![]() x2+
x2+![]() +3
+3![]() 与x轴交于C、D两点(点C在点D的左侧).
与x轴交于C、D两点(点C在点D的左侧).
(1)将点C向右平移![]() 个单位得到点E,过点E作直线l⊥x轴,点P为y轴上一动点,过点P作PQ⊥y轴交直线l于点Q,点K为抛物线上第一象限内的一个动点,当△ABK面积最大时,求KQ+QP+PE的最小值,及此时点P的坐标;
个单位得到点E,过点E作直线l⊥x轴,点P为y轴上一动点,过点P作PQ⊥y轴交直线l于点Q,点K为抛物线上第一象限内的一个动点,当△ABK面积最大时,求KQ+QP+PE的最小值,及此时点P的坐标;
(2)在(1)的条件下,将线段PE绕点P逆时针旋转90°后得线段PE′,问:在第一象限内是否存在点S,使得△SPE'是有一个角为60°,且以线段PE′为斜边的直角三角形,若存在请直接写出所有满足条件的点S,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC、∠ADC的平分线分別交CD、AB上点E、F.

(1)若∠ABC=∠ADC,求征:∠ADF=∠ABE;
(2)如图,若∠A与∠C互朴,试探究∠ADF与∠ABE之同的数量夫系,并说明理由;

(3)如图,在(2)的条件下,当DA⊥AB时,试探究BE与DF的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在![]() 中,
中,![]() 是高,
是高,![]() 是角平分线,当
是角平分线,当![]() ,
,![]() ,则
,则![]() ____
____![]() ;
;

(2)若![]() 和
和![]() 的度数分别用字母
的度数分别用字母![]() 和
和![]() 来表示(
来表示(![]() ),你能找到
),你能找到![]() 与
与![]() 和
和![]() 之间的关系吗? ______.(请直接写出你发现的结论)
之间的关系吗? ______.(请直接写出你发现的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com