
·ÖĪö £Ø1£©øł¾ŻĢāŅāæÉŅŌĮŠ³öĻąÓ¦µÄ·ÖŹ½·½³Ģ£¬“Ó¶ųæÉŅŌ½ā“š±¾Ģā£»
£Ø2£©øł¾ŻĢāŅāæÉŅŌĮŠ³öĻąÓ¦µÄ²»µČŹ½£¬“Ó¶ųæÉŅŌĒóµĆŠ”ĶõÖĮÉŁĒåµć¶ąÉŁ±¾Ķ¼Źé²ÅÄÜĄėæŖ£®
½ā“š ½ā£ŗ£Ø1£©É芔ĶõĘ½¾łĆæ·ÖÖÓĒåµćĶ¼Źéx±¾£¬
$\frac{300}{x}=\frac{200}{x-5}$£¬
½āµĆ£¬x=15£¬
¾¼ģŃéx=15ŹĒŌ·ÖŹ½·½³ĢµÄ½ā£¬
¼“Š”ĶõĘ½¾łĆæ·ÖÖÓĒåµćĶ¼Źé15±¾£»
£Ø2£©Š”ĶõĒåµćy±¾Ķ¼Źé²ÅÄÜĄėæŖ£¬
$\frac{3600-y}{10}”Ü3”Į60$£¬
½āµĆ£¬y”Ż1800£¬
¼“Š”ĶõÖĮÉŁĒåµć1800±¾Ķ¼Źé²ÅÄÜĄėæŖ£®
µćĘĄ ±¾Ģāæ¼²é·ÖŹ½·½³ĢµÄÓ¦ÓĆ”¢Ņ»ŌŖŅ»“Ī²»µČŹ½µÄÓ¦ÓĆ£¬½ā“š±¾ĢāµÄ¹Ų¼üŹĒĆ÷Č·ĢāŅā£¬ĮŠ³öĻąÓ¦µÄ·½³ĢŗĶ²»µČŹ½£¬×¢Ņā·ÖŹ½·½³ĢŅŖ¼ģŃ飮



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
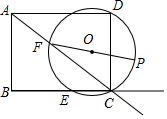 ČēĶ¼£¬¾ŲŠĪABCDµÄ±ßAB=3cm£¬AD=4cm£¬µćE“ÓµćB³ö·¢£¬ŃŲÉäĻßBCŅĘ¶Æ£¬¹żD”¢C”¢EČżµć×÷”ŃO£¬µćFĪŖ”ŃOÓėÉäĻßACµÄ¹«¹²µć£¬¹żF×÷”ŃOµÄÖ±¾¶FP£®µ±Ō²OÓėÉäĻßACĻąĒŠŹ±£¬µćEĶ£Ö¹ŅĘ¶Æ£¬ŌŚµćEŅĘ¶ÆµÄ¹ż³ĢÖŠ£¬µćPŅʶÆĀ·¾¶µÄ³¤£Ø””””£©
ČēĶ¼£¬¾ŲŠĪABCDµÄ±ßAB=3cm£¬AD=4cm£¬µćE“ÓµćB³ö·¢£¬ŃŲÉäĻßBCŅĘ¶Æ£¬¹żD”¢C”¢EČżµć×÷”ŃO£¬µćFĪŖ”ŃOÓėÉäĻßACµÄ¹«¹²µć£¬¹żF×÷”ŃOµÄÖ±¾¶FP£®µ±Ō²OÓėÉäĻßACĻąĒŠŹ±£¬µćEĶ£Ö¹ŅĘ¶Æ£¬ŌŚµćEŅĘ¶ÆµÄ¹ż³ĢÖŠ£¬µćPŅʶÆĀ·¾¶µÄ³¤£Ø””””£©| A£® | $\frac{15}{4}$ | B£® | $\frac{15}{4}$¦Š | C£® | $\frac{15}{2}$ | D£® | $\frac{15}{2}$¦Š |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| ŌĖĶłµŲ ³µŠĶ | ¼×µŲ£ØŌŖ/Į¾£© | ŅŅµŲ£ØŌŖ/Į¾£© |
| “ó»õ³µ | 720 | 800 |
| Š”»õ³µ | 500 | 650 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
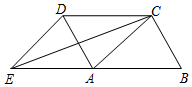 ČēĶ¼£¬ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬ŃÓ³¤BAµ½µćE£¬Ź¹AE=AB£¬ĮŖ½įED”¢EC”¢AC£®Ģķ¼ÓŅ»øöĢõ¼ž£¬ÄÜŹ¹ĖıߊĪACDE³ÉĪŖĮāŠĪµÄŹĒ£Ø””””£©
ČēĶ¼£¬ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬ŃÓ³¤BAµ½µćE£¬Ź¹AE=AB£¬ĮŖ½įED”¢EC”¢AC£®Ģķ¼ÓŅ»øöĢõ¼ž£¬ÄÜŹ¹ĖıߊĪACDE³ÉĪŖĮāŠĪµÄŹĒ£Ø””””£©| A£® | AB=AD | B£® | AB=ED | C£® | CD=AE | D£® | EC=AD |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
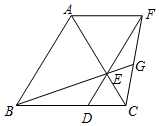 ČēĶ¼£¬ŅŃÖŖ”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬µćD”¢E·Ö±šŌŚ±ßBC”¢ACÉĻ£¬ĒŅCD=CE£¬ĮŖ½įDE²¢ŃÓ³¤ÖĮµćF£¬Ź¹EF=AE£¬ĮŖ½įAF£¬CF£¬ĮŖ½įBE²¢ŃÓ³¤½»CFÓŚµćG£®
ČēĶ¼£¬ŅŃÖŖ”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬µćD”¢E·Ö±šŌŚ±ßBC”¢ACÉĻ£¬ĒŅCD=CE£¬ĮŖ½įDE²¢ŃÓ³¤ÖĮµćF£¬Ź¹EF=AE£¬ĮŖ½įAF£¬CF£¬ĮŖ½įBE²¢ŃÓ³¤½»CFÓŚµćG£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
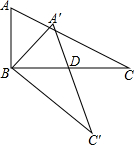 ČēĶ¼£¬”÷ABCÖŠ£¬”ĻABC=90”ć£¬AB=2£¬BC=4£¬ĻÖ½«”÷ABCČʶ„µćBĖ³Ź±Õė·½ĻņŠż×Ŗ”÷A”äBC”äµÄĪ»ÖĆ£¬“ĖŹ±A”äC”äÓėBCµÄ½»µćDŹĒBCµÄÖŠµć£¬ŌņĻ߶ĪC”äDµÄ³¤¶ČŹĒ£Ø””””£©
ČēĶ¼£¬”÷ABCÖŠ£¬”ĻABC=90”ć£¬AB=2£¬BC=4£¬ĻÖ½«”÷ABCČʶ„µćBĖ³Ź±Õė·½ĻņŠż×Ŗ”÷A”äBC”äµÄĪ»ÖĆ£¬“ĖŹ±A”äC”äÓėBCµÄ½»µćDŹĒBCµÄÖŠµć£¬ŌņĻ߶ĪC”äDµÄ³¤¶ČŹĒ£Ø””””£©| A£® | $\frac{4\sqrt{5}}{5}$ | B£® | $\frac{6\sqrt{5}}{5}$ | C£® | $\frac{8\sqrt{5}}{5}$ | D£® | 2$\sqrt{5}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | B£® | 3$\sqrt{5}$”Į2$\sqrt{3}$=6$\sqrt{15}$ | C£® | £Ø2$\sqrt{2}$£©2=8 | D£® | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com