
【题目】已知在矩形ABCD中,AB=4,AD=3,⊙C与对角线BD相切.
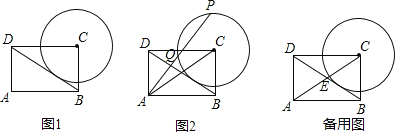
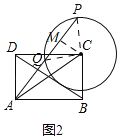
(1)如图1,求⊙C的半径;
(2)如图2,点P是⊙C上一个动点,连接AP,AC,AP交⊙C于点Q,若sin∠PAC=![]() ,求∠CPA的度数和弧PQ的长;
,求∠CPA的度数和弧PQ的长;
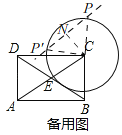
(3)如图,对角线AC与⊙C交于点E,点P是⊙C上一个动点,设点P到直线AC的距离为d,当0<d≤![]() 时,请直接写出∠PCE度数的取值范围.
时,请直接写出∠PCE度数的取值范围.
【答案】(1)![]() ;(2)60°,
;(2)60°,![]() ;(3)0°<∠PCE≤60°或120°≤∠PCE<180°
;(3)0°<∠PCE≤60°或120°≤∠PCE<180°
【解析】
(1)先利用勾股定理求出BD,再用三角形的面积公式求解即可得出结论;
(2)先根据三角函数求出CM和∠CPM,进而求出∠PCQ,最后用弧长公式计算即可得出结论;
(3)先判断出0<CN≤![]() ,再利用三角函数求出分界点CN=
,再利用三角函数求出分界点CN=![]() 时的∠PCE的度数,即可得出结论.
时的∠PCE的度数,即可得出结论.
(1)如图1,在矩形ABCD中,CD=AB=4,BC=AD=3,∠BCD=90°,
设切点为H.连接CH,
∵ BD与⊙C相切于H,
∴ CH⊥BD,
根据勾股定理得,BD=![]() ,
,
∵ S△BCD=![]() BCCD=
BCCD=![]() BDCH,
BDCH,
∴ CH=![]() ,
,
即⊙C的半径为![]() ;
;
(2)如图2,连接CP,CQ,过点C作CM⊥AP于M,
∵ 四边形ABCD是矩形,
∴ AC=BD=5,
在Rt△ACM中,sin∠PAC=![]() ,
,
∴ CM=![]() ,
,
在Rt△CMP中,sin∠CPM=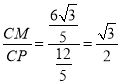 ,
,
∴∠CPM=60°,
即∠CPA=60°,
∵ CP=CQ,
∴ △CPQ是等边三角形,
∴ ∠ PCQ=60°,
∴ 弧PQ的长为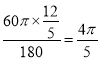 ;
;
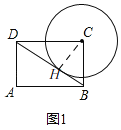
(3)如图备用图,过点P作PP'∥AC,过点C作CN⊥PP'于N,
则∠PCN=∠P'CN,∠ECN=∠CNP=90°,
∴ 点P到AC的距离d=CN,
∵ 0<d≤![]() ,
,
∴ 0<CN≤![]() ,
,
当CN=0时,点P在直线AC上,∠PCE=0°,
当CN=![]() 时,连接CP,CP',
时,连接CP,CP',
在Rt△P'CN中,cos∠P'CN=![]() =
=![]() =
=![]() ,
,
∴ ∠P'CN=30°,
∴ ∠PCN=∠P'CN=30°
∴ ∠P'CE=∠ECN﹣∠P'CN=60°,∠PCE=∠ECN+∠PCN=120°,
∴ ∠PCE度数的取值范围为0°<∠PCE≤60°或120°≤∠PCE<180°


科目:初中数学 来源: 题型:
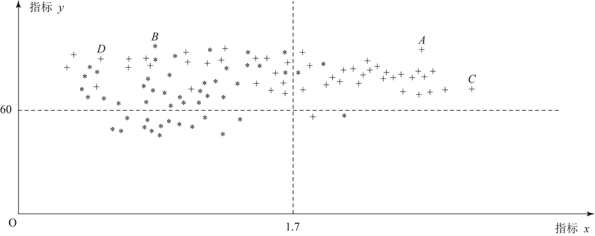
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
科目:初中数学 来源: 题型:
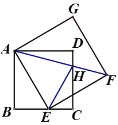
【题目】如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFG,对角线AF交边CD于H,连EH.①BE+DH=EH;②若E为BC的中点,则H为CD的中点;③EF平分∠HEC;④![]() .其中正确的序号是_______.
.其中正确的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
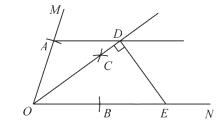
【题目】如图,已知![]() 是一个锐角,以点
是一个锐角,以点![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,画射线
,画射线![]() .过点
.过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设
.设![]() ,
,![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
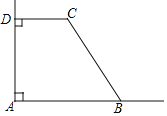
【题目】如图所示,AB⊥AD于点A,CD⊥AD于点D,∠C=120°.若线段BC与CD的和为12,则四边形ABCD的面积可能是( )
A.24![]() B.30
B.30![]() C.45D.
C.45D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级组织有奖知识竞赛,派小明去购买A、B两种品牌的钢笔作为奖品.已知一支A品牌钢笔的价格比一支B品牌钢笔的价格多5元,且买100元A品牌钢笔与买50元B品牌钢笔数目相同.
(1)求A、B两种品牌钢笔的单价分别为多少元?
(2)根据活动的设奖情况,决定购买A、B两种品牌的钢笔共100支,如果设购买A品牌钢笔的数量为n支,购买这两种品牌的钢笔共花费y元.
①直接写出y(元)关于n(支)的函数关系式;
②如果所购买A品牌钢笔的数量不少于B品牌钢笔数量的![]() ,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°![]() α
α![]() 360°),请判断并证明线段BE与线段CD的数量关系;
360°),请判断并证明线段BE与线段CD的数量关系;
(3)解决问题
将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°![]() α
α![]() 360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数 .
360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;
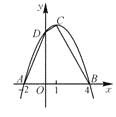
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量![]() (单位:件)与线下售价
(单位:件)与线下售价![]() (单位:元/件,
(单位:元/件,![]() )满足一次函数的关系,部分数据如下表:
)满足一次函数的关系,部分数据如下表:

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当![]() 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com