
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
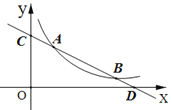
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
【答案】(1)![]() ;(2)2<x<8;(3)点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.
;(2)2<x<8;(3)点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.
【解析】
(1)首先确定A、B两点坐标,再利用待定系数法即可解决问题;
(2)观察图象,根据A、B两点的横坐标即可确定.
(3)分两种情形讨论求解即可.
解:(1)∵点A(m,4)和点B(8,n)在![]() 图象上,
图象上,
∴![]() ,即A(2,4),B(8,1)
,即A(2,4),B(8,1)
把A(2,4),B(8,1)两点代入![]() 得
得
![]() 解得:
解得: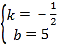 ,所以直线AB的解析式为:
,所以直线AB的解析式为:![]()
(2)由图象可得,当x>0时,![]() 的解集为2<x<8.
的解集为2<x<8.
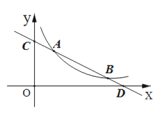
(3)由(1)得直线AB的解析式为![]() ,当x=0时,y=5,当y=0时,x=10,即C点坐标为(0,5),D点坐标为(10,0)
,当x=0时,y=5,当y=0时,x=10,即C点坐标为(0,5),D点坐标为(10,0)
∴OC=5,OD=10,![]()
∴![]()
设P点坐标为(a,0),由题可以,点P在点D左侧,则PD=10-a
由∠CDO=∠ADP可得
①当![]() 时,△COD∽△APD,此时AP∥CO,
时,△COD∽△APD,此时AP∥CO,![]() ,解得a=2,
,解得a=2,
故点P坐标为(2,0)
②当![]() 时,△COD∽△PAD,即
时,△COD∽△PAD,即![]() ,解得a=0,
,解得a=0,
即点P的坐标为(0,0)
因此,点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
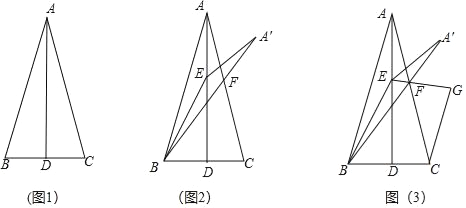
【题目】已知:AD是△ABC的高,且BD=CD.
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
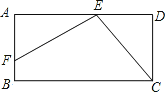
【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
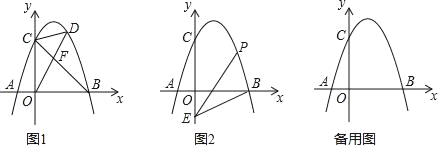
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
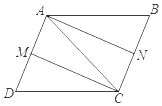
【题目】已知:如图,在平行四边形ABCD中,M、N分别是AD和BC的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=CD,求证四边形AMCN是矩形;
(3)若∠ACD=90°,求证四边形AMCN是菱形;
(4)若AC=CD,∠ACD=90°,求证四边形AMCN是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品,若按每件5元的价格销售,每天能卖出300件,若按每件6元的价格销售,每天能卖出200件,假定每天销售件数![]() (件)与价格
(件)与价格![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)令每天的利润为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式;当销售价格定为多少时,才能使每天的利润最大?每天最大利润是多少?
之间的函数关系式;当销售价格定为多少时,才能使每天的利润最大?每天最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com