
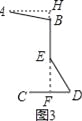
����Ŀ��ͼ1��һ�ֿ��۵�̨�ƣ���������ˮƽ�����ϣ���������ͼ2�����е�B��E��D��Ϊ��ת���㣮�ֲ��AB=BE=ED=CD=15cm������ε��Է��ֵ���B��E����ֱ�ߴ�ֱ����CD���е�Fʱ����ͼ3��ʾ�����ý�ƽ�ȣ�
��1����ƽ�ȷ���ʱ����DC��Ƹ�DE�ļнǵĴ�С��
��2��Ϊ����������д��ʱ�۾�������ľ���Ӧ������30cm��Ϊ��ֹ̨�ƴ��ۣ���A������ľ���Ӧ������30cm����̨��ƽ�ȷ���ʱ��ABE�����ֵ���������ȷ��0.01�����ο����ݣ� ![]() ��1.732��sin7.70���0.134��cos82.30���0.134����ʹ�ÿ�ѧ��������
��1.732��sin7.70���0.134��cos82.30���0.134����ʹ�ÿ�ѧ��������

���𰸡�(1)��60����(2)��97.34��.
�����������������(1)��������ã�DF=![]() CD=7.5cm��EF��CD���������Ǻ����Ķ��弴�ɵõ����ۣ�(2)����ͼ3����A��AH��BE��EB���ӳ�����H�����EF=15��
CD=7.5cm��EF��CD���������Ǻ����Ķ��弴�ɵõ����ۣ�(2)����ͼ3����A��AH��BE��EB���ӳ�����H�����EF=15��![]() =
=![]() ������cos��ABH=
������cos��ABH=![]() ��0.134�����ݵõ����ۣ�
��0.134�����ݵõ����ۣ�
���������(1)��������ã�DF=![]() CD=
CD=![]() cm��EF��CD�� ��cosD=
cm��EF��CD�� ��cosD=![]() �� ���D=60����
�� ���D=60����
��ƽ�ȷ���ʱ����DC��Ƹ�DE�ļн���60����
(2)����ͼ3����A��AH��BE��EB���ӳ�����H�� ��HF=30�� ��EF=15��![]() =
=![]() ��
��
��BH=30��BE��EF=15��![]() �� ��cos��ABH=
�� ��cos��ABH=![]() ��0.134�� ���ABH��82.26���� ���ABE=97.34����
��0.134�� ���ABH��82.26���� ���ABE=97.34����
��̨��ƽ�ȷ���ʱ��ABE�����ֵ��97.34����


 ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʶ��������ѧϰ�����ͼʱ�������á� ![]() ����ʾ�������롢������á�
����ʾ�������롢������á� ![]() ����ʾ���ݴ�����������á�
����ʾ���ݴ�����������á� ![]() ����ʾ�����жϿ�����������ִ������·���е�ijһ����
����ʾ�����жϿ�����������ִ������·���е�ijһ���� 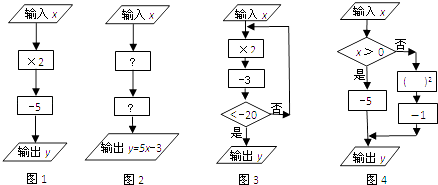
�����Խ����
��1������ͼ1����������x=��2ʱ�������y=��
����ͼ2����һ���� ![]() ���ڣ�Ӧ���� �ڶ�����
���ڣ�Ӧ���� �ڶ����� ![]() ���ڣ�Ӧ����
���ڣ�Ӧ����
��2������ͼ3����������x=��1ʱ�������y=������ͼ4���������ֵy=17���������ֵx=��
��3��Ϊ������Լ��ˮ����������ˮʵ�С����ݼۡ�����ÿ����ˮ��������10��ʱ����10�֣�����3Ԫ/�ֵļ۸��շѣ���ÿ����ˮ������10��ʱ������������4Ԫ/�ֵļ۸��շѣ�����Ƴ�һ���������ͼ����ʹ��������Ϊ��ˮ��x�������Ϊˮ��y��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵���Ҫ�����ס���������Ʒ��160��������ۺ��ۼ����±���(ע������=�ۼۣ�����)

(1)���̵�ƻ�������������Ʒ���ܻ���1 100Ԫ�����ʼס���������ƷӦ�ֱ����ټ���
(2)���̵�ƻ�Ͷ���ʽ�����4300Ԫ����������������Ʒ���������1260Ԫ���������ļ��ֹ�����������ָ���������Ĺ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶��4��OP=3�����P���O��λ�ù�ϵ�ǣ� ��
A.��P��Բ��
B.��P��Բ��
C.��P��Բ��
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵ��������Σ�AB=AC��
��1���������Σ���ͼ1����DE��BCʱ����DB������������EC������������������������=����
��2������̽��������ͼ1�е���ADE�Ƶ�A˳ʱ����ת����0��������180������ͼ2λ�ã���1���еĽ��ۻ��������������������֤����������������˵�����ɣ�
��3����չ���ã���ͼ3��P�ǵ���ֱ��������ABC��һ�㣬��ACB=90������PB=1��PC=2��PA=3������BPC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M��1��=��2��M��2��=����2��������2����M��3��=����2��������2��������2��������M��n��= ![]()
��1����գ�M��5��= �� M��50�� ��һ�����������������
��2�����㣺��2M��6��+M��7������4M��7��+2M��8����
��3��ֱ��д��2016M��n��+1008M��n+1����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=BC����ABC=90�㣬��ABΪֱ���ġ�O��OC���D��AD���ӳ��߽�BC�ڵ�E����D����O�����߽�BC�ڵ�F�����н��ۣ���CD2=CE��CB����4EF 2=ED ��EA���ۡ�OCB=��EAB����![]() ��������ȷ��ֻ��____________________��������ţ�
��������ȷ��ֻ��____________________��������ţ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com