
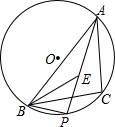
 如图,已知BC是⊙O的一条弦,点A是⊙0的优弧BC上的一个动点(点A与B,C不重合),∠BAC的平分线AP交⊙O于点P.∠ABC的平分线BE交AP于点E,连结BP.
如图,已知BC是⊙O的一条弦,点A是⊙0的优弧BC上的一个动点(点A与B,C不重合),∠BAC的平分线AP交⊙O于点P.∠ABC的平分线BE交AP于点E,连结BP.分析 (1)由于AP平分∠BAC,即∠BAP=∠CAP,则根据圆周角定理可得$\widehat{PB}$=$\widehat{PC}$,于是可判断点P为$\widehat{BC}$的中点;
(2)通过证明PE=PB来判断PE的长度不会随点A的运动而变化.
解答 (1)证明:∵∠BAC的平分线AP交⊙O于点P,
即∠BAP=∠CAP,
∴$\widehat{PB}$=$\widehat{PC}$,
∴点P为$\widehat{BC}$的中点;
(2)解:PE的长度不会随点A的运动而变化.理由如下: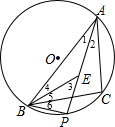 如图,
如图,
∵BE平分∠ABC,
∴∠4=∠5,
∵∠3=∠1+∠4,
而∠1=∠2,
∴∠3=∠5+∠2,
∵∠2=∠6,
∴∠3=∠5+∠6,
∴PE=PB,
∴PE的长度不会随点A的运动而变化.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等腰三角形的判断和圆周角定理.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:填空题
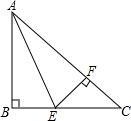 如图,在Rt△ABC中,∠ABC=90°,AE是角平分线,若BE:EC=3:5,BC=4cm,则点E到AC的距离为$\frac{3}{2}$cm.
如图,在Rt△ABC中,∠ABC=90°,AE是角平分线,若BE:EC=3:5,BC=4cm,则点E到AC的距离为$\frac{3}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com