
分析 直接根据题意将原式化简进而结合分式的性质得出n的值.
解答 解:∵f(1)=$\frac{1}{1×(1+1)}$=$\frac{1}{1×2}$=1-$\frac{1}{2}$,
f(2)=$\frac{1}{2×(2+1)}$=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$…,
∴f(1)+f(2)+f(3)+…+f(n)=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{2017}{2018}$,
∴$\frac{n}{n+1}$=$\frac{2017}{2018}$,
故n=2017.
故答案为:2017.
点评 此题主要考查了函数值以及分式的计算,正确将原式变形是解题关键.


科目:初中数学 来源: 题型:解答题
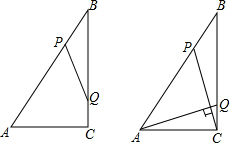 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
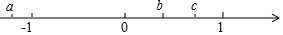 在数轴上和有理数a、b、c对应的点的位置如图所示:
在数轴上和有理数a、b、c对应的点的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0除以任何数都得0 | |
| B. | 若a<-1,则$\frac{1}{a}$<a | |
| C. | 同号两数相除,取原来的符号,并把两数的绝对值相除 | |
| D. | 若0<a<1,则$\frac{1}{a}$>a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
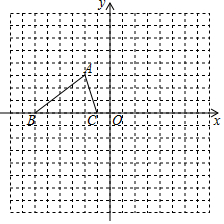 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
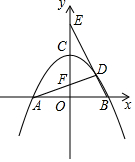 如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com