
【题目】四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF。
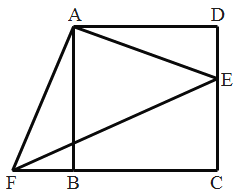
(1)求证:△ADE≌△ABF
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针方向旋转________度得到;
(3)若BC=8,DE=3,求△AEF的面积
【答案】(1)详见解析;(2)A,90; (3)36.5
【解析】
(1)根据正方形的性质得AD=AB,∠D=∠ABC=90°,然后利用“SAS”易证得△ADE≌△ABF;
(2)观察图形可得;
(3)先利用勾股定理可计算出AE=![]() ,再根据旋转的性质得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
,再根据旋转的性质得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
(1)证明:∵四边形ABCD为正方形
∴AD=AB,∠D=∠ABF=90°
∵DE=BF
∴△AFB≌△AED(SAS)
(2)观察图形可知:△ABF可以由△ADE绕旋转中心点A,按顺时针方向旋转 90度得到.
故答案为:A,90.
(3)S△AEF=S梯AFCD-S△ADE-S△EFC=![]() -
-![]() -
-![]() =36.5
=36.5


科目:初中数学 来源: 题型:
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好![]() 每人只能选其中一项
每人只能选其中一项![]() ,并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
,并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
![]() 在这次考察中一共调查了______名学生,请补全条形统计图;
在这次考察中一共调查了______名学生,请补全条形统计图;
![]() 被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.
被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
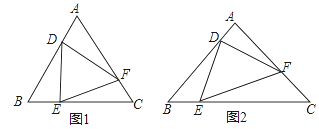
【题目】定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=![]() ,求CF和AD的长.
,求CF和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
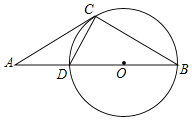
【题目】如图,点A是⊙O直径BD延长线上的一点,AC是⊙O的切线,C为切点.AD=CD,
(1)求证:AC=BC;
(2)若⊙O的半径为1,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3.
(1)求它的对称轴和顶点坐标;
(2)求该抛物线与x轴的交点坐标;
(3)建立平面直角坐标系,画出这条抛物线的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com