
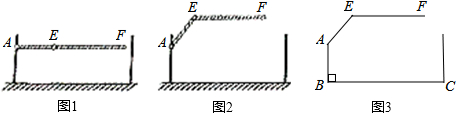
分析 过点E作EG⊥BC于点G,AH⊥EG于点H,则∠AHE=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AE•sin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
解答 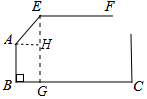 解:过点E作EG⊥BC于点G,AH⊥EG于点H.
解:过点E作EG⊥BC于点G,AH⊥EG于点H.
∵EF∥BC,
∴∠GEF=∠BGE=90°
∵∠AEF=143°,
∴∠AEH=53°.
∴∠EAH=37°.
在△EAH中,AE=1.2,∠AHE=90°,
∴sin∠EAH=sin 37°
∴$\frac{EH}{AE}≈0.6$
∴EH=1.2×0.6=0.72.
∵AB⊥BC,
∴四边形ABGH为矩形.
∵GH=AB=1.2,
∴EG=EH+HG=1.2+0.72=1.92≈1.9.
答:适合该地下车库的车辆限高标志牌为1.9米.
点评 本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
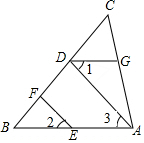 如图,EF⊥BC,AD⊥BC,∠1=∠2,∠B=30°.求∠GDB的度数.
如图,EF⊥BC,AD⊥BC,∠1=∠2,∠B=30°.求∠GDB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-1 | B. | x≤3 | C. | 1<x≤3 | D. | -1<x≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
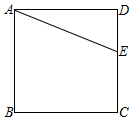 如图,点E是正方形ABCD的边CD上一点,把线段AE沿EC方向平移,使得点E与点C重合,得到线段CF.
如图,点E是正方形ABCD的边CD上一点,把线段AE沿EC方向平移,使得点E与点C重合,得到线段CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com