
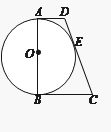
【题目】如图,AB为⊙O的直径,AD与⊙O相切于一点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
⑴求证:BC为⊙O的切线;
⑵若AB=2![]() ,AD=2,求线段BC的长.
,AD=2,求线段BC的长.
【答案】![]()
【解析】
试题(1)因为BC经过圆的半径的外端,只要证明AB⊥BC即可.连接OE、OC,利用△OBC≌△OEC,得到∠OBC=90°即可证明BC为⊙O的切线.
(2)作DF⊥BC于点F,构造Rt△DFC,利用勾股定理解答即可.
试题解析:(1)证明:连接OE、OC.
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
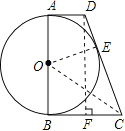
(2)解:过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2![]() .
.
∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2![]() )2,解得x=
)2,解得x=![]() .
.
∴BC=![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB交AB于点D;∠CAE=∠B.
(1)如果AC=3.5 cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的三个顶点在边长为1的正方形网格中,已知
的三个顶点在边长为1的正方形网格中,已知![]() ,
,![]() ,
,![]() .
.
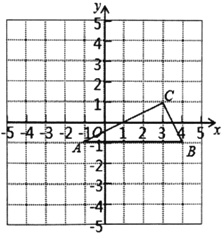
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的对应点,不写画法);
的对应点,不写画法);
(2)分别写出![]() ,
,![]() ,
,![]() 三点的坐标.
三点的坐标.
(3)请写出所有以![]() 为边且与
为边且与![]() 全等的三角形的第三个顶点(不与
全等的三角形的第三个顶点(不与![]() 重合)的坐标_____.
重合)的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
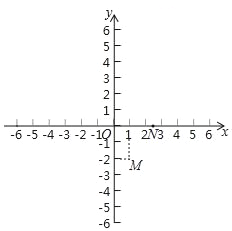
【题目】已知抛物线y=ax2+bx+c(x为任意实数)经过下图中两点M(1,﹣2)、N(m,0),其中M为抛物线的顶点,N为定点.下列结论:
①若方程ax2+bx+c=0的两根为x1,x2(x1<x2),则﹣1<x1<0,2<x2<3;
②当x<m时,函数值y随自变量x的减小而减小.
③a>0,b<0,c>0.
④垂直于y轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为s、,则s+t=2.
其中正确的是( )
A. ①② B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
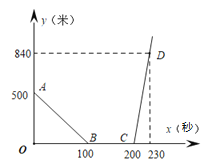
【题目】小明和妈妈开车去中央公园采风,小明爸爸发现他们忘记带画笔后立即开车追赶他们.假设妈妈和爸爸的车在同一直线公路上匀速行驶,当爸爸的车追上妈妈的车后,两车停下来,爸爸把画笔交给小明.然后小明和妈妈开车以原来速度的![]() 倍继续前行,爸爸则以来时一半的速度沿原路回家.设小明爸爸开车的时间为
倍继续前行,爸爸则以来时一半的速度沿原路回家.设小明爸爸开车的时间为![]() (秒),两车间的距离为
(秒),两车间的距离为![]() (米),
(米),![]() 关于
关于![]() 的部分函数关系如图所示,当小明爸爸回到家时,小明和妈妈正好行驶了全程的
的部分函数关系如图所示,当小明爸爸回到家时,小明和妈妈正好行驶了全程的![]() ,则小明家离中央公园的距离为________米
,则小明家离中央公园的距离为________米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com