
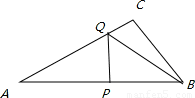
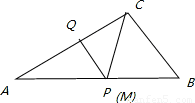
��ͼ����Rt��ABC�У���C=90�㣬AB=10cm��AC��BC=4��3����P�ӵ�A������AB�������B�˶����ٶ�Ϊ1cm/s��ͬʱ��Q�ӵ�B������B��C��A�������A�˶����ٶ�Ϊ2cm/s����һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶���
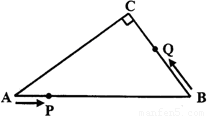
��1����AC��BC�ij���
��2�����P���˶�ʱ��Ϊx���룩����PBQ�����Ϊy��cm2��������PBQ����ʱ����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3������Q��CA���˶���ʹPQ��ABʱ���Ե�B��P��QΪ��������������ABC�Ƿ����ƣ���˵�����ɣ�
��4����x=5��ʱ����ֱ��PQ���Ƿ����һ��M��ʹ��BCM���ܳ���С�������ڣ������С�ܳ����������ڣ���˵�����ɣ�
8,6��0��x��3��16
��������
��������� ��1����AC=4x��BC=3x����Rt��ABC��AC2+BC2=AB2��
������4x��2+��3x��2=102����ã�x=2����AC=8cm��BC=6cm��
��2���ٵ���Q�ڱ�BC���˶�ʱ������Q��QH��AB��H��
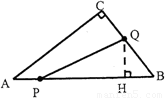
��AP=x����BP=10��x��BQ=2x���ߡ�QHB�ס�ACB��
��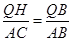 ��
��
��QH=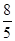 x��y=
x��y=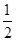 BP?QH=
BP?QH=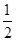 ��10��x��?
��10��x��?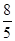 x=��
x=��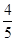 x2+8x��0��x��3����
x2+8x��0��x��3����
�ڵ���Q�ڱ�CA���˶�ʱ������Q��QH���AB��H�䣬
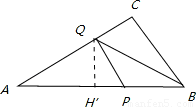
��AP=x��
��BP=10��x��AQ=14��2x���ߡ�AQH��ס�ABC��
��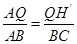 ������
������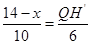 ����ã�QH��=
����ã�QH��=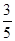 ��14��x����
��14��x����
��y=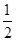 PB?QH��=
PB?QH��=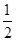 ��10��x��?
��10��x��?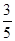 ��14��x��=
��14��x��=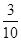 x2��
x2��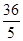 x+42��3��x��7����
x+42��3��x��7����
��y��x�ĺ�����ϵʽΪ��y=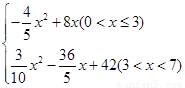 ��
��
��3����AP=x��AQ=14��x��
��PQ��AB�����APQ�ס�ACB��
��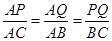 ������
������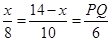 ��
��
��ã�x=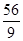 ��PQ=
��PQ=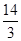 ����PB=10��x=
����PB=10��x=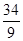 ����
����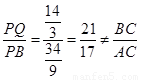 ��
��
�൱��Q��CA���˶���ʹPQ��ABʱ���Ե�B��P��QΪ��������������ABC�����ƣ�
��4�����ڣ�
���ɣ���AQ=14��2x=14��10=4��AP=x=5����AC=8��AB=10��
��PQ�ǡ�ABC����λ�ߣ���PQ��AB����PQ��AC��
��PQ��AC�Ĵ�ֱƽ���ߣ���PC=AP=5��
�൱��M��P�غ�ʱ����BCM���ܳ���С��
���BCM���ܳ�Ϊ��MB+BC+MC=PB+BC+PC=5+6+5=16�����BCM���ܳ���С.
���㣺���κ������ۺ���
���������⽫�ô���ϵ��������κ�������ʽ�������������Сֵ�������ϣ��нϴ��˼ά��Ծ��������ͬѧ�ǵ�Ӧ���������ۺ�˼ά��������һ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•�����ʼ죩��ͼ����Rt��ABC�У���C=90�㣬��BAC��ƽ����AD��BC�ڵ�D����E��AB��һ�㣬��AEΪֱ���ġ�O����D���ҽ�AC�ڵ�F��
��2013•�����ʼ죩��ͼ����Rt��ABC�У���C=90�㣬��BAC��ƽ����AD��BC�ڵ�D����E��AB��һ�㣬��AEΪֱ���ġ�O����D���ҽ�AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��AD��BD�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ������ཻ�ڵ�D�����D��BC�ľ��룮
��ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��AD��BD�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ������ཻ�ڵ�D�����D��BC�ľ��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �����ƶ���ʹ���30��ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ��
�����ƶ���ʹ���30��ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 |
 ��P���A���غ�ʱ������P��PQ��AC�ڵ�Q����PQΪ����������PQMN��ʹ��M�����߶�AC�ϣ����P���˶�ʱ��Ϊt��s����
��P���A���غ�ʱ������P��PQ��AC�ڵ�Q����PQΪ����������PQMN��ʹ��M�����߶�AC�ϣ����P���˶�ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com