
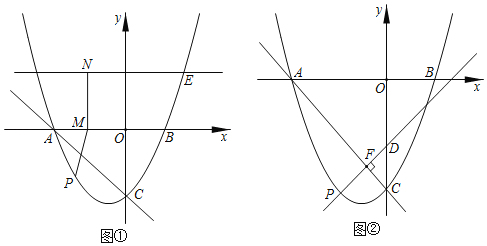
【题目】如图,抛物线y=![]() x2+x﹣4与x轴交于A,B(A在B的左侧),与y轴交于点C,抛物线上的点E的横坐标为3,过点E作直线l1∥x轴.
x2+x﹣4与x轴交于A,B(A在B的左侧),与y轴交于点C,抛物线上的点E的横坐标为3,过点E作直线l1∥x轴.
(1)点P为抛物线上的动点,且在直线AC的下方,点M,N分别为x轴,直线l1上的动点,且MN⊥x轴,当△APC面积最大时,求PM+MN+![]() EN的最小值;
EN的最小值;
(2)过(1)中的点P作PD⊥AC,垂足为F,且直线PD与y轴交于点D,把△DFC绕顶点F旋转45°,得到△D'FC',再把△D'FC'沿直线PD平移至△D″F′C″,在平面上是否存在点K,使得以O,C″,D″,K为顶点的四边形为菱形?若存在直接写出点K的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,点K的坐标为(
;(2)存在,点K的坐标为(![]() ,﹣
,﹣![]() )或(2+
)或(2+![]() ,﹣2﹣
,﹣2﹣![]() ).
).
【解析】
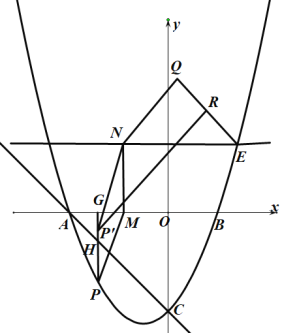
(1)过点P作PG⊥x轴于点G,交AC于点H,在PG上截取PP'=MN,连接P'N,以NE为斜边在直线NE上方作等腰Rt△NEQ,过点P'作P'R⊥EQ于点R,先利用二次函数的解析式求出A,B,C,E的坐标,然后用待定系数法求出直线AC的解析式,利用E点坐标得出PP'=MN=![]() ,然后设出点P(t,
,然后设出点P(t,![]() t2+t﹣4)H(t,﹣t﹣4),用含t的代数式表示出△APC的面积,利用二次函数的性质求出△APC的面积最大时对应的点P,
t2+t﹣4)H(t,﹣t﹣4),用含t的代数式表示出△APC的面积,利用二次函数的性质求出△APC的面积最大时对应的点P,![]() 的坐标,然后利用平行四边形和等腰直角三角形的性质得出PM+MN+
的坐标,然后利用平行四边形和等腰直角三角形的性质得出PM+MN+![]() EN=PP'+P'N+ NQ=
EN=PP'+P'N+ NQ=![]() +P'N+NQ,所以当点P'、N、Q在同一直线上时,P'N+NQ=P'R最小,即PM+MN+
+P'N+NQ,所以当点P'、N、Q在同一直线上时,P'N+NQ=P'R最小,即PM+MN+![]() EN=
EN=![]() +P'R,分别用待定系数法求出直线
+P'R,分别用待定系数法求出直线![]() 的表达式,联立求出点R的坐标,最后利用勾股定理求出
的表达式,联立求出点R的坐标,最后利用勾股定理求出![]() 的长度,则答案可求;
的长度,则答案可求;
(2)先求出D,F点的坐标,得出△CDF是等腰直角三角形,然后分两种情况讨论:把△DFC绕顶点F逆时针旋转45°,得到![]() ,经过分析发现以O,
,经过分析发现以O,![]() ,K为顶点的四边形为菱形,
,K为顶点的四边形为菱形,![]() 不可能为边,只能以
不可能为边,只能以![]() 为邻边构成菱形,然后利用菱形的性质即可求解;把△DFC绕顶点F顺时针旋转45°,得到△D'FC',以O,
为邻边构成菱形,然后利用菱形的性质即可求解;把△DFC绕顶点F顺时针旋转45°,得到△D'FC',以O,![]() ,K为顶点的四边形为菱形,
,K为顶点的四边形为菱形,![]() 只能为对角线,从而求出K的坐标即可.
只能为对角线,从而求出K的坐标即可.
(1)如图1,过点P作PG⊥x轴于点G,交AC于点H,在PG上截取PP'=MN,连接P'N,
以NE为斜边在直线NE上方作等腰Rt△NEQ,过点P'作P'R⊥EQ于点R
∵x=0时,y=![]() x2+x﹣4=﹣4
x2+x﹣4=﹣4
∴C(0,﹣4)
∵y=0时,![]() x2+x﹣4=0
x2+x﹣4=0
解得:x1=﹣4,x2=2
∴A(﹣4,0),B(2,0)
设直线AC的解析式为![]()
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线AC解析式为![]()
∵抛物线上的点E的横坐标为3
∴yE=![]() ×32+3﹣4=
×32+3﹣4=![]()
∴E(3,![]() ),直线l1:y=
),直线l1:y=![]()
∵点M在x轴上,点N在直线l1上,MN⊥x轴
∴PP'=MN=![]()
设抛物线上的点P(t,![]() t2+t﹣4)(﹣4<t<0)
t2+t﹣4)(﹣4<t<0)
∴H(t,﹣t﹣4)
∴PH=﹣t﹣4﹣(![]() t2+t﹣4)=﹣
t2+t﹣4)=﹣![]() t2﹣2t
t2﹣2t
∴S△APC=S△APH+S△CPH=![]() PHAG+
PHAG+![]() PHOG=
PHOG=![]() PHOA=2PH=﹣t2﹣4t
PHOA=2PH=﹣t2﹣4t
∴当t=﹣![]() =﹣2时,S△APC最大
=﹣2时,S△APC最大
∴yP=![]() t2+t﹣4=2﹣2﹣4=﹣4,yP'=yP+
t2+t﹣4=2﹣2﹣4=﹣4,yP'=yP+![]()
∴P(﹣2,﹣4),P'(﹣2,![]() )
)
∵PP'=MN,PP'∥MN
∴四边形PMNP'是平行四边形
∴PM=P'N
∵等腰Rt△NEQ中,NE为斜边
∴∠NEQ=∠ENQ=45°,NQ⊥EQ
∴NQ=![]() EN
EN
∴PM+MN+![]() EN=PP'+P'N+ NQ=
EN=PP'+P'N+ NQ=![]() +P'N+NQ
+P'N+NQ
∵当点P'、N、Q在同一直线上时,P'N+NQ=P'R最小
∴PM+MN+![]() EN=
EN=![]() +P'R
+P'R
设直线EQ解析式为y=﹣x+a
∵E(3,![]() )
)
∴﹣3+a=![]()
解得:a=![]()
∴直线EQ:y=﹣x+![]()
设直线P'R解析式为y=x+b
∵P'(﹣2,![]() )
)
∴﹣2+b=﹣![]()
解得:b=![]()
∴直线P'R:y=x+![]()
∵ 解得:
解得:![]()
∴R(![]() ,4)
,4)
∴P'R=
∴PM+MN+![]() EN最小值为
EN最小值为![]()
(2)∵PD⊥AC,P(﹣2,﹣4),
∴直线PD解析式为:y=x﹣2,
∴D(0,﹣2),F(﹣1,﹣3),
∴CD=2,DF=CF=![]() ,△CDF是等腰直角三角形,
,△CDF是等腰直角三角形,
如图2,把△DFC绕顶点F逆时针旋转45°,得到![]() ,
,
∴![]() (
(![]() ,﹣3),
,﹣3),![]() (﹣1,
(﹣1,![]() ﹣3)
﹣3)
把![]() 沿直线PD平移至
沿直线PD平移至![]() ,连接
,连接![]()
设直线![]() 的解析式为
的解析式为![]()
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线![]() 解析式为y=x﹣2﹣
解析式为y=x﹣2﹣![]() ,
,
同理:直线![]() 解析式为y=x+
解析式为y=x+![]() ﹣2,
﹣2,
显然OC″≥![]() +1>2=C″D″
+1>2=C″D″
∴以O,![]() ,K为顶点的四边形为菱形,
,K为顶点的四边形为菱形,![]() 不可能为边,只能以
不可能为边,只能以![]() 为邻边构成菱形
为邻边构成菱形
∴![]() ,
,
∵OK∥![]() ,PD⊥
,PD⊥![]() ,
,
∴OK⊥PD
∴K1(![]() ,﹣
,﹣![]() ),
),
如图3,把△DFC绕顶点F顺时针旋转45°,得到△D'FC',
∴![]() (﹣1,﹣3﹣
(﹣1,﹣3﹣![]() ),
),![]() (
(![]() ﹣1,﹣
﹣1,﹣![]() ﹣3)
﹣3)
把![]() 沿直线PD平移至
沿直线PD平移至![]() ,连接
,连接![]() ,
,![]() ,
,
显然,![]() ∥PD,
∥PD,![]() ≥
≥![]() +1>
+1>![]() ,
,![]() ≥
≥![]() +1>
+1>![]() ,
,
∴以O,![]() ,K为顶点的四边形为菱形,
,K为顶点的四边形为菱形,![]() 只能为对角线,
只能为对角线,
∴K2(2+![]() ,﹣2﹣
,﹣2﹣![]() ).
).
综上所述,点K的坐标为:K1(![]() ,﹣
,﹣![]() ),K2(2+
),K2(2+![]() ,﹣2﹣
,﹣2﹣![]() ).
).


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
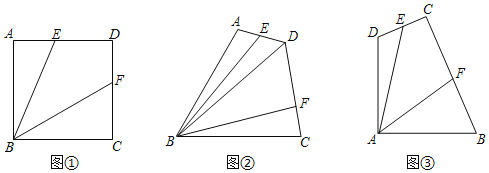
【题目】提出问题:(1)如图①,正方形ABCD中,点E,点F分别在边AD和边CD上,若正方形边长为4,DE+DF=4,则四边形BEDF的面积为 .
探究问题:(2)如图②,四边形ABCD,AB=BC=4,∠ABC=60°,∠ADC=120°,点E、F分别是边AD和边DC上的点,连接BE,BF,若ED+DF=3,BD=2![]() ,求四边形EBFD的面积;
,求四边形EBFD的面积;
解决问题:(3)某地质勘探队为了进行资源助测,建立了如图③所示的一个四边形野外勘查基地,基地相邻两侧边界DA、AB长度均为4km,∠DAB=90°,由于勘测需要及技术原因,主勘测仪C与基地边缘D、B夹角为90°(∠DCB=90°),在边界CD和边界BC上分别有两个辅助勘测仪E和F,辅助勘测仪E和F与主勘测仪C的距离之和始终等于4km(CE+CF=4).为了达到更好监测效果,需保证勘测区域(四边形EAFC)面积尽可能大.请问勘测区域面积有没有最大值,如果有求出最大值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
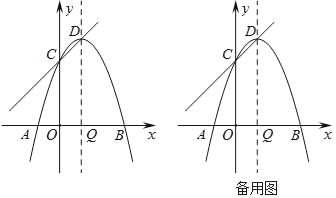
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
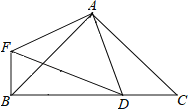
【题目】如图,△ABC与△AFD为等腰直角三角形,∠FAD=∠BAC=90°,点D在BC上,则:
(1)求证:BF=DC.
(2)若BD=AC,则求∠BFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
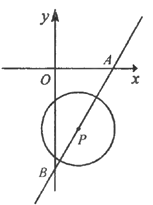
【题目】己知:如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 是直线
是直线![]() 上一动点,⊙
上一动点,⊙![]() 的半径为2.
的半径为2.
(1)判断原点![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当⊙![]() 与
与![]() 轴相切时,求出切点的坐标.
轴相切时,求出切点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
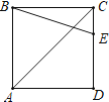
【题目】如图,AC为正方形ABCD的对角线,点E为DC边上一点(不与C、D重合),连接BE,以E为旋转中心,将线段EB逆时针旋转90°,得到线段EF,连接DF.
(1)请在图中补全图形.
(2)求证:AC∥DF.
(3)探索线段ED、DF、AC的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
(1)求证:△ABD∽△DCE;
(2)若CD=12,CE=3,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com