
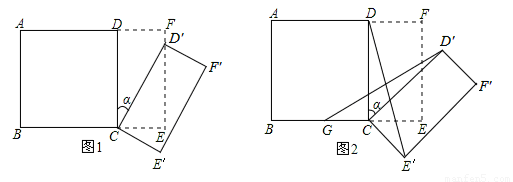
��ͼ1��ʾ����һ���߳�Ϊ2��������ABCD��һ����Ϊ2����Ϊ1�ij�����CEFDƴ��һ�𣬹���һ����ij�����ABEF���ֽ�С������CEFD�Ƶ�C˳ʱ����ת��CE��F��D�䣬��ת��Ϊa��
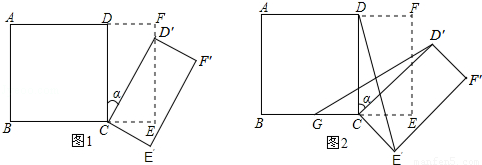
��1������D��ǡ������EF����ʱ������ת��a��ֵ��
��2����ͼ2��GΪBC�е㣬��0�㣼a��90�㣬��֤��GD��=E��D��
��3��С������CEFD�Ƶ�C˳ʱ����תһ�ܵĹ����У���DCD�����CBD���ܷ�ȫ�ȣ����ܣ�ֱ��д����ת��a��ֵ��������˵�����ɣ�
��1��30�㣻��2������������; ��3��135���315��.
��������
�����������1��������ת�����ʵ�CD��=CD=2����Rt��CED���У�CD��=2��CE=1�����CD��E=30�㣬Ȼ�����ƽ���ߵ����ʼ��ɵõ��Ϧ�=30�㣻
��2����GΪBC�е�ɵ�CG=CE��������ת�����ʵá�D��CE��=��DCE=90�㣬CE=CE�䣬���GCD��=��DCE��=90��+����Ȼ����ݡ�SAS�����жϡ�GCD��ա�DCE�䣬
��GD��=E��D��
��3�����������ε����ʵ�CB=CD����CD=CD�䣬���BCD�����DCD��Ϊ����ȵ������������Σ������������ʱ����ȫ�ȣ�����BCD�����DCD��Ϊ�۽�������ʱ���ɼ������=135�㣬����BCD�����DCD��Ϊ���������ʱ���ɼ���õ���=315�㣮
�����������1���߳�����CEFD�Ƶ�C˳ʱ����ת��CE��F��D�䣬
��CD��=CD=2��
��Rt��CED����CD��=2��CE=1��
���CD��E=30�㣬
��CD��EF��
��Ϧ�=30�㣻
��2����GΪBC�е㣬
��CG=1��
��CG=CE��
�߳�����CEFD�Ƶ�C˳ʱ����ת��CE��F��D�䣬
���D��CE��=��DCE=90�㣬CE=CE��=CG��
���GCD��=��DCE��=90��+����
�ڡ�GCD��͡�DCE����
 ��
��
���GCD��ա�E��CD��SAS����
��GD��=E��D��
��3���ܣ��������£�
���ı���ABCDΪ�����Σ�
��CB=CD��
��CD=CD�䣬
���BCD�����DCD��Ϊ����ȵ������������Σ�
����BCD��=��DCD��ʱ����BCD��ա�DCD�䣬
����BCD�����DCD��Ϊ�۽�������ʱ����=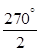 =135�㣬
=135�㣬
����BCD�����DCD��Ϊ���������ʱ����=360�㩁 =315�㣬
=315�㣬
����ת��a��ֵΪ135���315��ʱ����BCD�����DCD��ȫ�ȣ�
���㣺 1.��ת�����ʣ�2.ȫ�������ε��ж������ʣ�3.���ε����ʣ�4.�����ε����ʣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ�ɽ��Ϋ��������ѧ���������� ���ͣ������
��ͼ1��ʾ����һ���߳�Ϊ2��������ABCD��һ����Ϊ2����Ϊ1�ij�����CEFDƴ��һ�𣬹���һ����ij�����ABEF.�ֽ�С������CEFD�Ƶ�C˳ʱ����ת��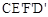 ,��ת��Ϊ
,��ת��Ϊ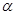 .
.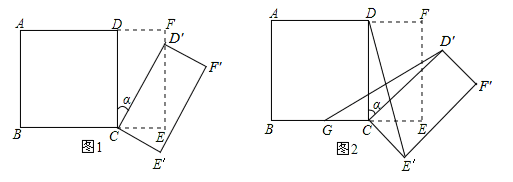
��1������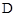 ǡ������EF����ʱ������ת��
ǡ������EF����ʱ������ת��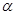 ��ֵ��
��ֵ��
��2����ͼ2��GΪBC���е㣬��00��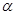 ��900����֤��
��900����֤��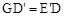 ��
��
��3��С������CEFD�Ƶ�C˳ʱ����תһ�ܵĹ����У� ��
��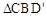 �ܷ�ȫ�ȣ����ܣ�ֱ��д����ת��
�ܷ�ȫ�ȣ����ܣ�ֱ��д����ת��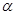 ��ֵ�������ܣ�˵������.
��ֵ�������ܣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ�ɽ��Ϋ��������ѧ�������棩 ���ͣ������
��ͼ1��ʾ����һ���߳�Ϊ2��������ABCD��һ����Ϊ2����Ϊ1�ij�����CEFDƴ��һ�𣬹���һ����ij�����ABEF.�ֽ�С������CEFD�Ƶ�C˳ʱ����ת��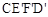 ,��ת��Ϊ
,��ת��Ϊ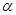 .
.
��1������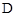 ǡ������EF����ʱ������ת��
ǡ������EF����ʱ������ת��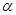 ��ֵ��
��ֵ��
��2����ͼ2��GΪBC���е㣬��00��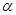 ��900����֤��
��900����֤�� ��
��
��3��С������CEFD�Ƶ�C˳ʱ����תһ�ܵĹ����У� ��
��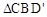 �ܷ�ȫ�ȣ����ܣ�ֱ��д����ת��
�ܷ�ȫ�ȣ����ܣ�ֱ��д����ת��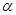 ��ֵ�������ܣ�˵������.
��ֵ�������ܣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013��ɽ��ʡΫ�����п���ѧ�Ծ��������棩 ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com