若一元二次方程x2-2x-k=0无实数根,则二次函数y=x2+(k+1)x+k的图象的顶点在( )
A.第四象限
B.第三象限
C.第二象限
D.第一象限
【答案】
分析:先由一元二次方程x
2-2x-k=0无实数根得出,∴△=4+4k<0,从而得出k的取值范围,再求出二次函数y=x
2+(k+1)x+k的△的取值范围,则此题易解.
解答:解:∵一元二次方程x
2-2x-k=0无实数根,
∴△=4+4k<0,即k<-1,则二次函数y=x
2+(k+1)x+k的图象与x轴没有交点,对称轴的横坐标x=-
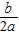
=-
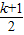
>0,与y轴交点为(0,k),故函数图象的顶点第四象限.
故选A.
点评:二次函数和一元一次方程有以下关系:方程有两个不相等的实数根,二次函数的图象与x轴有两个交点;方程有两个相等的实数根,二次函数的图象与x轴有1个交点;方程没有实数根,二次函数的图象与x轴没有交点.

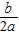 =-
=-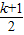 >0,与y轴交点为(0,k),故函数图象的顶点第四象限.
>0,与y轴交点为(0,k),故函数图象的顶点第四象限.
