
【题目】关于x的方程:2(x﹣k)=x﹣4①和关于x的一元二次方程:(k﹣1)x2+2mx+(3﹣k)+n=0②(k、m、n均为实数),方程①的解为非正数.
(1)求k的取值范围;
(2)如果方程②的解为负整数,k﹣m=2,2k﹣n=6且k为整数,求整数m的值;
(3)当方程②有两个实数根x1、x2,满足(x1+x2)(x1﹣x2)+2m(x1﹣x2+m)=n+5,且k为正整数,试判断|m|≤2是否成立?请说明理由.
【答案】(1)k≤2且k≠1;(2)m=﹣2或﹣3;(3)成立,见解析
【解析】
(1)先解出方程①的解,根据一元二次方程的定义和方程①的根为非正数,得出k的取值范围,即可;
(2)先把k=m+2,n=2m﹣2代入方程②化简,通过因式分解法,用含m的代数式表示出一元二次方程的两个实数根,根据方程②的解为负整数,m为整数,即可求出m的值;
(3)根据(1)中k的取值范围和k为正整数得出k=2,化简一元二次方程,并将两根和与积代入计算,得出关于m、n的等式,结合根的判别式,即可得到结论.
(1)∵关于x的方程:2(x﹣k)=x﹣4,
解得:x=2k﹣4,
∵关于x的方程2(x﹣k)=x﹣4的解为非正数,
∴2k﹣4≤0,解得:k≤2,
∵由一元二次方程②,可知k≠1,
∴k≤2且k≠1;
(2)∵一元二次方程(k﹣1)x2+2mx+(3﹣k)+n=0中k﹣m=2,2k﹣n=6,
∴k=m+2,n=2k﹣6=2m+4﹣6=2m﹣2,
∴把k=m+2,n=2m﹣2代入原方程得:(m+1)x2+2mx+m﹣1=0,
因式分解得,[(m+1)x+(m﹣1)](x+1)=0,
∴x1=﹣![]() =
=![]() ,x2=﹣1,
,x2=﹣1,
∵方程②的解为负整数,m为整数,
∴m+1=﹣1或﹣2,
∴m=﹣2或﹣3;
(3)|m|≤2成立,理由如下:
由(1)知:k≤2且k≠1,
∵k是正整数,
∴k=2,
∵(k﹣1)x2+2mx+(3﹣k)+n=0有两个实数根x1、x2,
∴x1+x2=![]() =﹣2m,x1x2=
=﹣2m,x1x2=![]() =1+n,
=1+n,
∵(x1+x2)(x1﹣x2)+2m(x1﹣x2+m)=n+5,
∴2m2=n+5 ①,
△=(2m)2﹣4(k﹣1)[(3﹣k)+n]=4m2﹣4(n+1)≥0 ②,
把①代入②得:4m2﹣8m2+16≥0,即m2≤4,
∴|m|≤2.


科目:初中数学 来源: 题型:
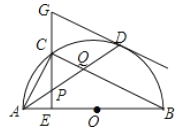
【题目】如图,在![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() ,交于下列结论:
,交于下列结论:
①![]() ;
;
②![]() ;
;
③点![]() 是
是![]() 的外心,
的外心,
④![]()
其中正确结论是_________________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx+3=0(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C
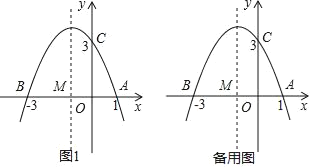
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,请问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() 的顶点
的顶点![]() 是底边
是底边![]() 的中点,两边分别与
的中点,两边分别与![]() 交于点
交于点![]() .
.
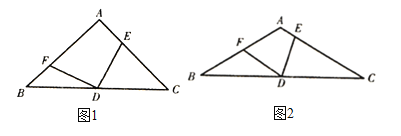
(1)如图1,![]() ,当
,当![]() 的位置变化时,
的位置变化时,![]() 是否随之变化?证明你的结论;
是否随之变化?证明你的结论;
(2)如图2,当![]() ,当
,当![]() °时,(1)中的结论仍然成立,求出此时
°时,(1)中的结论仍然成立,求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
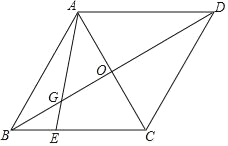
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
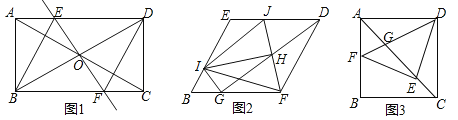
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,且BD=DE,过点B作BP∥DE,交⊙O于点P,连结OP.
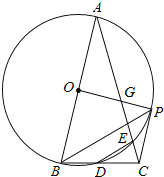
(1)求证:AB=AC;
(2)若∠A=30°,求∠BOP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+bx+c (a≠0)的顶点为M (1,9), 经过抛物线上的两点A(-3,-7)和B (3, m)的直线交抛物线的对称轴于点C.

(1)求抛物线的解析式和直线AB的解析式;
(2)在抛物线上是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点A、M、P、Q为顶点的四边形是平行四边形时,直接写出满足足条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com