
【题目】某水果店以10元/千克的价格收购一批农产品进行销售,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 10 | 13 | 16 | 19 | 22 | |
日销售量y(千克) | 100 | 85 | 70 | 55 | 40 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定y与x之间的函数表达式;
(2)若该水果店要获得375元的日销售利润,销售单价x应定为多少元?
(3)该水果店应该如何确定这批水果的销售价格,才能使日销售利润W最大?并求出最大利润.
【答案】(1)y= -5x+150 ;(2)x1=25, x2=15;(3)定为20元,最大利,500元
【解析】
(1)首先根据表中的数据,可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,解出x的值即为所求;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可.
(1)假设y与x成一次函数关系,设函数关系式为y=kx+b,
则![]()
解得:k=-5,b=150,
∴y=-5x+150,
检验:当x=13,y =85;当x=16,y =70;当x=19,y =55,符合一次函数解析式;
(2)设日销售利润为W,则
W=(x-10)(- 5x+150)
∴(x-10)(- 5x+150)=375
∴x1=25, x2=15
即销售单价x应定为25元或15元.
(3)根据题意得,W=(x-10)(- 5x+150)= - 5x2 +200x-1500= - 5(x-20)2+500
∴ x=20时,Wmax=500
即水果店这批水果的销售价格为20元时,才能使日销售利润W最大,最大利润为500元.


科目:初中数学 来源: 题型:
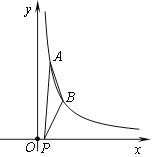
【题目】如图,双曲线![]() (x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为_______________.
(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C是AB延长线上的一点,点D在⊙O上且AD=CD,∠C=30°.
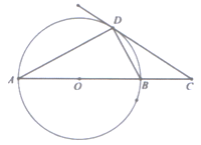
(1)求证:CD是⊙O的切线,
(2)若⊙O的半径为5,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为( )
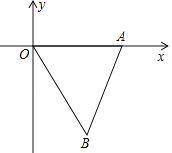
A.(8,﹣12)B.(﹣8,12)
C.(8,﹣12)或(﹣8,12)D.(5,﹣12)
查看答案和解析>>
科目:初中数学 来源: 题型:
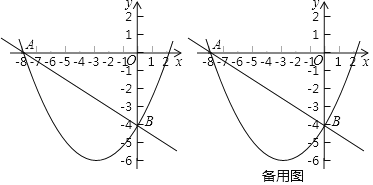
【题目】在平面直角坐标系中,抛物线y=ax2+bx﹣4经过点A(﹣8,0),对称轴是直线x=﹣3,点B是抛物线与y轴交点,点M、N同时从原点O出发,以每秒1个单位长度的速度分别沿x轴的负半轴、y的负半轴方向匀速运动,(当点N到达点B时,点M、N同时停止运动).过点M作x轴的垂线,交直线AB于点C,连接CN、MN,并作△CMN关于直线MC的对称图形,得到△CMD.设点N运动的时间为t秒,△CMD与△AOB重叠部分的面积为S.
(1)求抛物线的函数表达式;
(2)当0<t<2时,
①求S与t的函数关系式.
②直接写出当t=_____时,四边形CDMN为正方形.
(3)当点D落在边AB上时,过点C作直线EF交抛物线于点E,交x轴于点F,连接EB,当S△CBE:S△ACF=1:3时,直接写出点E的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆从A站开往D站的动车,途中经停B、C两站,互不相识的甲、乙、丙三人同时从A站上车。
(1)求甲、乙两人在同一车站下车的概率;
(2)甲、乙、丙三人在同一车站下车的概率为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,且OA2为斜边在△OA1A2外作等腰直角△OA2A3,以OA3为斜边在△OA2A3外作等腰直角△OA3A4,以OA4为斜边在△OA3A4外作等腰直角△OA4A5,…连接A1A3,A3A5,A5A7,…分别与OA2,OA4,OA6,…交于点B1,B2,B3,…按此规律继续下去,记△OB1A3的面积为S1,△OB2A5的面积为S2,△OB3A7的面积为S3,…△OBnA2n+1的面积为Sn,则Sn=__(用含正整数n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
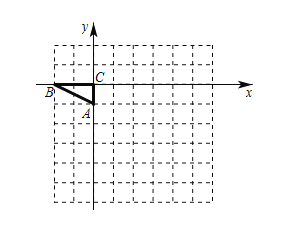
【题目】如图,平面直角坐标系中,以点C为坐标原点,点![]() ,
,![]() ,将
,将![]() 绕点A顺时针旋转90°.
绕点A顺时针旋转90°.
(1)在图中画出旋转后的![]() ,并写出点
,并写出点![]() 、
、![]() 的坐标;
的坐标;
(2)已知点![]() ,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出
,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出![]() 的最小值;
的最小值;
(3)写出![]() 在旋转过程中,线段AB扫过的面积
在旋转过程中,线段AB扫过的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com