
| A. | ①②③④ | B. | ①②④ | C. | ①②③ | D. | ①② |
分析 根据∠α与∠β互补,得出∠β=180°-∠α,∠α=180°-∠β,求出∠β的余角是90°-∠β,90°-∠β表示∠β的余角;∠α-90°=90°-∠β,即可判断②;180°-∠α=∠β,根据余角的定义即可判断③;求出$\frac{1}{2}$(∠α-∠β)=90°-∠β,即可判断④.
解答 解:∵∠α与∠β互补,
∴∠β=180°-∠α,∠α=180°-∠β,
∴90°-∠β表示∠β的余角,∴①正确;
∠α-90°=180°-∠β-90°=90°-∠β,∴②正确;
180°-∠α=∠β,∴③错误;
$\frac{1}{2}$(∠α-∠β)=$\frac{1}{2}$(180°-∠β-∠β)=90°-∠β,∴④错误;
故选D.
点评 本题考查了对余角和补角的理解和运用,关键是注意:∠α与∠β互补,得出∠β=180°-∠α,∠α=180°-∠β;∠β的余角是90°-∠β.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
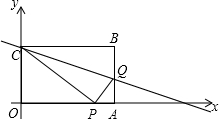 如图,在平面直角坐标系中,矩形OABC的直角边OA、OC分别在x轴的正半轴和y轴的正半轴上,过点C的直线y=-$\frac{1}{3}$x+a交矩形的AB边于点Q,AQ=b.
如图,在平面直角坐标系中,矩形OABC的直角边OA、OC分别在x轴的正半轴和y轴的正半轴上,过点C的直线y=-$\frac{1}{3}$x+a交矩形的AB边于点Q,AQ=b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
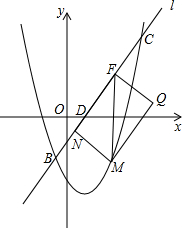 已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
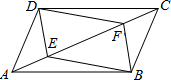 如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )
如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com