
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形? 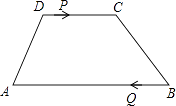
【答案】解:①以PQAD构成四边形 设X秒成为平行四边形
根据题意得:
x=24﹣3x
∴x=6
∴当运动6s时成为平行四边形;
②以PQBC构成四边形
设Y秒成为平行四边形
根据题意得:
10﹣y=3y
∴y=2.5
∴当运动2.5s时也成为平行四边形.
③四边形PAQC、四边形PDQB其实也可能成为平行四边形,其中,PDQB是错误的,四边形PAQC成为平行四边形时是7秒.
故答案为6秒、2.5秒、7秒
【解析】根据题意P,Q和梯形ABCD的两个顶点构成平行四边形,分两种情况讨论:①可以构成四边形PQAD;②可以构成四边形PQBC两种.
【考点精析】认真审题,首先需要了解平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( ) 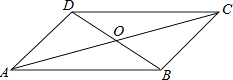
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形使纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)). A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.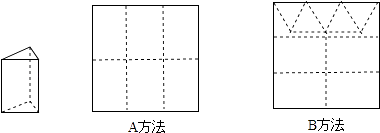
(1)分别求裁剪出的侧面和底面的个数(用x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:

(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com