
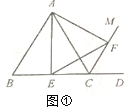
【题目】【感知】如图①,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC中点,在CM上截取CF=BE,连接AE、EF、AF.易证:△AEF是等边三角形(不需要证明).
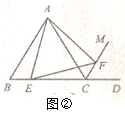
【探究】如图②,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC上一点(不与点B、C重合),在CM上截取CF=BE,连接AE、EF、AF.求证:△AEF是等边三角形.
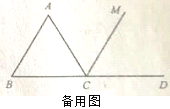
【应用】将图②中的“E是边BC上一点”改为“E是边BC延长线上一点”,其他条件不变.当四边形ACEF是轴对称图形,且AB=2时,请借助备用图,直接写出四边形ACEF的周长.
【答案】【探究】见解析;【应用】![]()
【解析】试题分析:【探究】根据等边三角形的性质和角平分线的性质证明△ABE≌△ACF,得到AE=AF,再证明∠EAF=60°,即可得到结论;
【应用】先证明△AEF为等边三角形,得到不可能以AE所在的直线为对称轴,只能以CF为对称轴,从而得到∠BAE=90°,以及AE的值,即可得到结论
试题解析:解:【探究】∵△ABC是等边三角形,∴AB=AC,∠B=∠ACB=60°,∴∠ACD=120°.∵CM是外角∠ACD的平分线,∴![]() ,∴∠B=∠ACF=60°.∵CF=BE,∴△ABE≌△ACF,∴AE=AF,∠BAE=∠CAF.∵∠BAC=60°,∴∠BAE+∠EAC=∠CAF +∠EAC,∴∠EAF=60°,∴△AEF是等边三角形.
,∴∠B=∠ACF=60°.∵CF=BE,∴△ABE≌△ACF,∴AE=AF,∠BAE=∠CAF.∵∠BAC=60°,∴∠BAE+∠EAC=∠CAF +∠EAC,∴∠EAF=60°,∴△AEF是等边三角形.
【应用】由题意得:△ABE≌△ACF,∴AE=AF,∠BAE=∠CAF,∴∠FAE=∠BAC=60°,∴△AEF为等边三角形,∴AE=AF=EF,∴不可能以AE所在的直线为对称轴,即以CF为对称轴.∵AB=2,∴AC=CE=2,∴AC=BC=CE,∴∠BAE=90°,∴AE=![]() ,∴四边形ACEF的周长为:
,∴四边形ACEF的周长为: ![]() =
=![]() .
.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
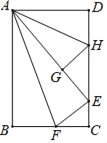
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8,则点Q的运动路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
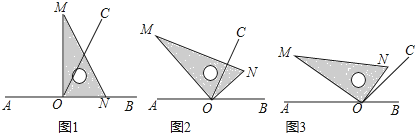
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批西服,进价为每套250元,原定每套以290元的价格销售,这样每天可销售200套.如果每套比原销售价降低10元销售,则每天可多销售100套.该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论(每套西服的利润=每套西服的销售价﹣每套西服的进价).
(1)按原销售价销售,每天可获利润 元.
(2)若每套降低10元销售,每天可获利润 元.
(3)如果每套销售价降低10元,每天就多销售100套,每套销售价降低20元,每天就多销售200套.
按这种方式:
①若每套降低10x元,则每套的销售价格为 元;(用代数式表示)
②若每套降低10x元,则每天可销售 套西服.(用代数式表示)
③若每套降低10x元,则每天共可以获利润 元.(用代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将有规律的整数1,﹣2,3,﹣4,5,﹣6,…按照如图所示的方式排成数阵.
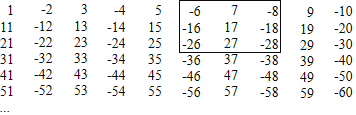
(1)用字母表示如图横行任意三个相邻的数的关系 、 、 .
(2)如图,方框中九个数之和与正中间数17有什么关系?请计算说明.
(3)用这样的方框在数阵中移动(一直保持框出数阵中的9个数),那么方框中九个数之和与正中间数关系,还如(2)中一样成立吗?请用字母解释其中所包含的规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
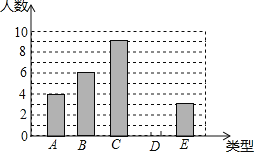
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.

(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,求P点坐标?
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com