
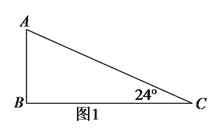
【题目】(![]() )如图
)如图![]() 中,
中,![]() ,请用直尺和圆规作一条直线,把
,请用直尺和圆规作一条直线,把![]() 分割成两个等腰三角形(不写作法,但须保留作图痕迹).
分割成两个等腰三角形(不写作法,但须保留作图痕迹).
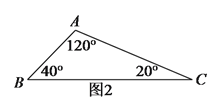
(![]() )如图
)如图![]() 中,
中,![]() 的三个内角分别为
的三个内角分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,在
,在![]() 上找一个点
上找一个点![]() ,使
,使![]() 为等腰三角形,求出
为等腰三角形,求出![]() 的长(可用含
的长(可用含![]() 的代数式表示).
的代数式表示).


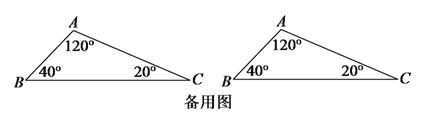
【答案】(1)图形见解析;(2)![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)尺规作图,作出BC的垂直平分线,将点C和中垂线与线段AB的交点连接起来即可;(2)要使△ABP为等腰三角形,由于没有明确指出腰和底,因此要分类讨论,分三类:①BP=BA,②AP=AB,③PA=PB,分别求出三种情况下BP的长即可.
试题解析:
(![]() )如图所示:直线
)如图所示:直线![]() 即为所求,
即为所求,
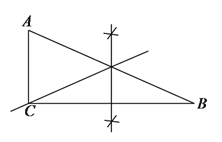
(![]() )①当BP=BA时,BP=4;
)①当BP=BA时,BP=4;

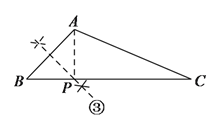
②当AP=AB时,∠APB=∠B=40°,
∴∠PAC=∠C=20°,
∴PA=PC=4,
∴BP=a-4;
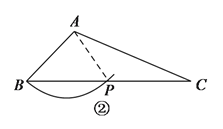
③当PA=PB时,∠BAP=∠B=40°,
∴∠CAP=∠CPA=80°,
∴CP=CA=6,
∴BP=a-6.
∴BP的长为4或a-4或a-6.


科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在CCTV“开心辞典”栏目中,主持人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是( )
A.-1
B.0
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边长,且满足a2+b2+c2=ab+bc+ac,则△ABC是( )
A. 等腰三角形B. 等边三角形
C. 直角三角形D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
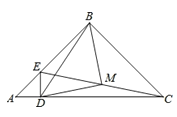
【题目】已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.
(1)求证:△BMD为等腰直角三角形;
(2)当点E运动多少秒时,△BMD的面积为12.5cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com