练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列关于二次函数的说法错误的是( )

    A.二次函数y=(x+2)2－2的顶点坐标是(－2,－2)

    B.抛物线y=－x2 +2x+1，当x<0时y随x的增大而增大

    C.函数y= 2x2 + 4x－3的图象的最低点坐标为(－1,－5)

    D.点A(3,0)不在抛物线y=x2－2x－3的图象上

    【答案】D

    【解析】

    根据抛物线的顶点坐标公式，对称轴，点的坐标与抛物线解析式的关系，逐一检验即可．

    解：A、二次函数y=(x+2)2－2的顶点坐标是(－2,－2)，故A正确；

    B、抛物线y=－x2 +2x+1，对称轴为：，则当x<1时，y随x的增大而增大，故当x<0时，y随x的增大而增大，正确；

    C、函数y= 2x2 + 4x－3的图象开口向上，对称轴为：，则函数的最低点坐标为：(－1,－5)；故C正确；

    D、当x=3时，代入抛物线，解得：y=0，故点A（3，0）在y=x2－2x－3的图象上，故D错误；

    故选择：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=6，AD=12，点E在AD边上，且AE=8，EF⊥BE交CD于F．

    （1）求证：△ABE∽△DEF；

    （2）求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问锯几何？”用现代的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意，CD长为（ ）

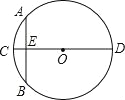
    A．12寸 B．13寸 C．24寸 D．26寸

    查看答案和解析>>

    科目：初中数学 来源： 题型：

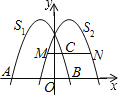
    【题目】如图，抛物线S1与x轴交于点A（﹣3，0），B（1，0），将它向右平移2个单位得新抛物线S2，点M，N是抛物线S2上两点，且MN∥x轴，交抛物线S1于点C，已知MN＝3MC，则点C的横坐标为（　　）

    A.B.C.D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

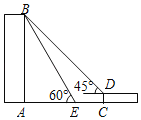
    【题目】在一次数学综合实践活动中，同学们测量了学校教学楼的高度．如图，CD是高为2m的平台，在D处测得楼顶B的仰角为45°，从平台底部向教学楼方向前进4m到达E处，测得楼顶B的仰角为60°．求教学楼AB的高度（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A的坐标为(3, 2)，点B的坐标为(3, 0). 作如下操作:①以点A为旋转中心，把△ABO顺时针旋转90°，得到△ACD;

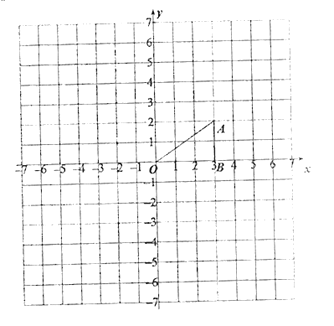
    (1)在图中画出△ACD;

    (2)①请直接写点B旋转到点C的路径长:____________；

    ②画出△ABO关于点O的中心对称图形△EOF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，⊙C的半径为r，给出如下定义：若点P的横、纵坐标均为整数，且到圆心C的距离d≤r，则称P为⊙C 的关联整点.

    （1）当⊙O的半径r=2时，在点D（2，-2），E（-1，0），F（0，2）中，为⊙O的关联整点的是 ；

    （2）若直线上存在⊙O的关联整点，且不超过7个，求r的取值范围；

    （3）⊙C的圆心在x轴上，半径为2，若直线上存在⊙C的关联整点，求圆心C的横坐标t的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

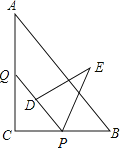
    【题目】如图，Rt△ABC中，∠C＝90°，AB＝15，BC＝9，点P，Q分别在BC，AC上，CP＝3x，CQ＝4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．

    （1）求证：PQ∥AB；

    （2）若点D在∠BAC的平分线上，求CP的长；

    （3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

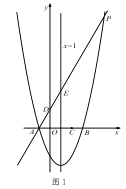
    【题目】如图1，对称轴为直线x=1的抛物线y=x2+bx+c，与x轴交于A、B两点（点A在点B的左侧），且点A坐标为(-1，0).又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与抛物线对称轴交于点E，点C与坐标原点O关于该对称轴成轴对称.

    （1）求点 B 的坐标和抛物线的表达式；

    （2）当 AE：EP=1：4 时，求点 E 的坐标；

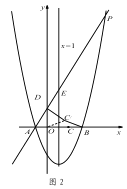
    （3）如图 2，在（2）的条件下，将线段 OC 绕点 O 逆时针旋转得到 OC ′，旋转角为 α(0°＜α＜90°)，连接 C ′D、C′B，求 C ′B+ C′D 的最小值．

    查看答案和解析>>

    同步练习册答案