
 已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,
已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,分析 (1)由AD∥BC得出∠ADB=∠DBC,再由AB=AD得出∠ADB=∠ABD,从而∠ABD=∠DBC,另外AE⊥BD,故∠AEB=∠C=90°,结论显然;
(2)作AF⊥BC于F,则AF=CD,FC=AD,算出BF,从而由勾股定理算出AF.
解答 解:(1)证明:
∵AD∥BC,
∴∠ADB=∠DBC,
∵AB=AD,
∴∠ADB=∠ABD,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DCB;
(2)作AF⊥BC于F,如图,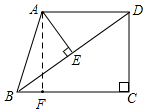
∵AD∥BC,∠C=90°,
∴AFCD是矩形,
∴FC=AD=50,AF=CD,
∴BF=BC-FC=64-50=14,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=48,
∴DC=48.
点评 本题主要考查了平行线的性质、等腰三角形的性质、相似三角形的判定与性质、矩形的判定与性质、勾股定理等知识点,属于基础题.熟练掌握基本几何图形和相关定理是解答关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com