
分析 根据抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=$\frac{1}{2x}$经过点(a,bc),可以得到a>0,a、b、c的关系,然后对a、b、c进行讨论,从而可以判断①②③④是否正确,本题得以解决.
解答 解:∵抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=$\frac{1}{2x}$经过点(a,bc),
∴$\left\{\begin{array}{l}{a>0}\\{a+b+c=1}\\{bc=\frac{1}{2a}}\end{array}\right.$
∴bc>0,故①正确;
∴x2+(a-1)x+$\frac{1}{2a}$=0可以转化为:x2-(b+c)x+bc=0,得x=b或x=c,故③正确;
∵b,c是关于x的一元二次方程x2+(a-1)x+$\frac{1}{2a}$=0的两个实数根,
∴△=(a-1)2-4×1×$\frac{1}{2a}$≥0,
化简,得(a-2)(a2+1)≥0,
∵a2+1≥1,
∴a-2≥0,
∴a≥2,
故a≥2,即2a-1≥3,故④正确;
∵a≥2且a+b+c=1,
∴b+c<0,故②错误;
故答案为:①③④.
点评 本题考查二次函数与图象的关系,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
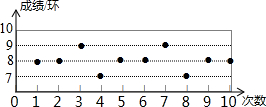 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.| 甲 | 乙 | 丙 | |
| 平均数 | 7.9 | 7.9 | 8.0 |
| 方差 | 3.29 | 0.49 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥1 | B. | m≤1 | C. | m≥0 | D. | m≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )
如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )| A. | 3 | B. | 4 | C. | 4.8 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com