Question

如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．

（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
（2）当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的；
（3）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．

Answer 1

（1）证明见解析;(2)当AP=2时, △ADQ的面积的面积是正方形ABCD面积的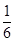;(3)当CP=4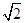-4时，△ADQ是等腰三角形.

解析试题分析：（1）正方形的对角线与边的夹角是45°,在正方形ABCD中，无论点P运动到AB上何处时，都有AD=AB,∠DAQ=∠BAQ,AQ=AQ,∴△ADQ≌△ABQ.(2)△ADQ的面积恰好是正方形ABCD面积的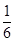时，过点Q作QE⊥AD于E,QF⊥AB于F，则QE =QF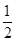，AD×QE=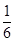S_{正方形ABCD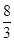}=,∴QE=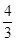,由△DEQ∽△DAP得,
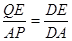解得AP=2,∴AP=2时，△ADQ的面积的面积是正方形ABCD面积的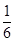.（3）若△ADQ是等腰三角形，则有QD=QA或DA=DQ或AQ=AD,①当点P运动到与点B重合时，由四边形ABCD是正方形知QD=QA,此时△ADQ是等腰三角形,②当点P与点C重合时，点Q与点C也重合，此时DA=DQ,△ADQ是等腰三角形.③如图，设点P在BC边上运动到CP=x时，有AD=AQ,∵AD∥BC,∴∠ADQ=∠CPQ,又∵∠AQD=∠CQP,∠ADQ=∠AQD,∴∠CQP=∠CPQ,∴CQ=CP=x,∵AC=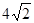,AQ=AD=4,∴z=CQ=AC-AQ=4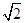-4,即当CP=4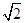-4时，△ADQ是等腰三角形.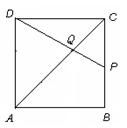

试题解析：（1）证明：在正方形ABCD中，无论点P运动到AB上何处时，都有AD=AB,∠DAQ=∠BAQ,AQ=AQ,
∴△ADQ≌△ABQ.
(2)解：△ADQ的面积恰好是正方形ABCD面积的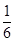时，
过点Q作QE⊥AD于E,QF⊥AB于F，
则QE=QF，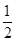
AD×QE=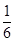S_{正方形ABCD}=,
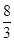∴QE=,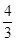
由△DEQ∽△DAP得,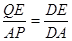
解得AP=2,
∴AP=2时，△ADQ的面积的面积是正方形ABCD面积的.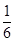
（3）若△ADQ是等腰三角形，则有QD=QA或DA=DQ或AQ=AD,
①当点P运动到与点B重合时，由四边形ABCD是正方形知QD=QA,
此时△ADQ是等腰三角形,
②当点P与点C重合时，点Q与点C也重合，
此时DA=DQ,△ADQ是等腰三角形.
③解：如图，设点P在BC边上运动到CP=x时，有AD=AQ,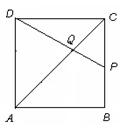

∵AD∥BC,
∴∠ADQ=∠CPQ,
又∵∠AQD=∠CQP,∠ADQ=∠AQD,
∴∠CQP=∠CPQ,
∴CQ=CP=x,
∵AC=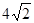,AQ=AD=4,
∴z=CQ=AC-AQ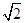=4-4,
即当CP=4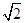-4时，△ADQ是等腰三角形.
考点：1.正方形;2.三角形的相似.