Question

5．在四边形ABCD中，已知AB=AD=CD=4，AD∥BC，∠B=60°，点E、F分别为边BC、CD上的两动点，且∠EAF=60°．
（1）求出四边形ABCD的面积．
（2）△AEF是否存在周长最小值？若存在，求出最小值．若不存在，说明理由．
（3）△AEF是否存在面积最小值？若存在，求出最小值．若不存在，说明理由．

Answer 1

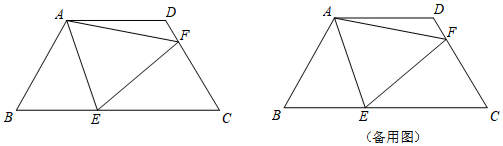
分析 （1）作辅助线，将四边形分成两个直角三角形和一个矩形，利用面积和可得四边形ABCD的面积；
（2）存在，如图2，根据轴对称的最短路径，作A关于BC、CD的对称点A'、A''，交BC于G，交直线CD于H，可知此时△AEF的周长最小；证明△EAF是等边三角形，又知A'E=AE=4，可得周长的最小值；
（3）存在，如图3，作辅助线，构建△AME≌△AFE，将△ADF绕点A顺时针旋转120°到△ABM，根据角的关系证明M、B、E共线，再证明△FAE≌△MAE，则∠MEA=∠FEA，过A作AH⊥BC于H，作AK⊥EF于K，根据角平分线的性质可知：AH=AK=2$\sqrt{3}$，作△AEF的外接圆⊙O，由同弧所对的圆心角是圆周角的二倍得：∠NOF=60°，设EF=2x，则NF=x，
根据OA+ON≥AK，列式为$\sqrt{3}$x≥2$\sqrt{3}$，则x≥2，可得△AEF面积的最小值是4$\sqrt{3}$．

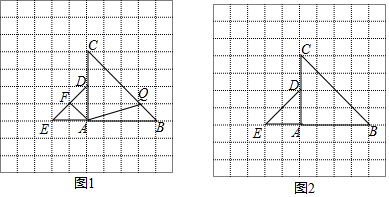
解答 解：（1）如图1，过A作AE⊥BC于E，过D作DF⊥BC于F，
∵AD∥BC，
∴∠BAD=180°-∠B=180°-60°=120°，
Rt△ABE中，∠BAE=30°，AB=4，
∴BE=2，AE=2$\sqrt{3}$，
∴∠EAD=120°-30°=90°，
∵∠AEF=∠EFD=90°，
∴四边形AEFD是矩形，
∵AB=DC，AE=DF，
∴Rt△ABE≌Rt△DCF（HL），
∴S_△ABE=S_△DCF，
∴S_{四边形ABCD}=2S_△ABE+S_矩形AEFD=2×$\frac{1}{2}$×2×2$\sqrt{3}$+4×$2\sqrt{3}$=12$\sqrt{3}$；
（2）存在，如图2，作A关于BC、CD的对称点A'、A''，交BC于G，交直线CD于H，
连接A'A''，交BC于E，交CD于F，此时△AEF的周长最小；
∵AB=AD=4，
∴由（1）可得：AG=AH=2$\sqrt{3}$，
∴AA'=AA''，
在四边形AGCH中，∵∠C=60°，∠AGC=∠AHC=90°，
∴∠A'AA''=120°，
∴∠A'=30°，
∵AE=A'E，
∴∠A'=∠A'AE=30°，
∴∠AEF=∠A'+∠A'AE=60°，
∵∠EAF=60°，
∴△EAF是等边三角形，
∵A'E=AE=4，
∴△AEF的周长=4×3=12，且此时F与D重合，
即△AEF存在周长最小值，最小值是12；
（3）存在，
如图3，将△ADF绕点A顺时针旋转120°到△ABM，
由旋转得：BM=DF，AM=AF，∠ABM=∠D=120°，∠MAB=∠FAD，
∵∠ABC=60°，
∴∠ABM+∠ABC=180°，
∴M、B、E共线，
∵∠MAE=∠MAB+∠BAE=∠FAD+∠BAE=60°，
∠EAF=60°，AE=AE，
∴△FAE≌△MAE，
∴∠MEA=∠FEA，
过A作AH⊥BC于H，作AK⊥EF于K，
∴AH=AK=2$\sqrt{3}$，
作△AEF的外接圆⊙O，连接OA、OE、OF，
过O作ON⊥EF，
∵∠EAF=60°，
∴∠EOF=120°，
∴∠NOF=60°，
设EF=2x，则NF=x，
Rt△ONF中，ON=$\frac{\sqrt{3}}{3}$x，OF=$\frac{2\sqrt{3}}{3}$x，
∴ON+OA=OF+ON=$\sqrt{3}$x，
∵OA+ON≥AK，
∴$\sqrt{3}$x≥2$\sqrt{3}$，
x≥2，
∴S_△AEF=$\frac{1}{2}$EF•AK=$\frac{1}{2}$$•2x•2\sqrt{3}$=2$\sqrt{3}$x≥4$\sqrt{3}$，
∴△AEF面积的最小值是4$\sqrt{3}$．

点评 本题是四边形的综合题，考查了角平分线的性质、等边三角形、三角形和四边形的面积、三角形全等的性质和判定、直角三角形30°角的性质、轴对称的最短路径问题等知识，本题主要求最值问题，此类有难度，确定其最值时动点的位置是关键．