
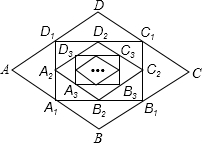
 如图,在菱形ABCD中,边长为10,∠A=60°,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是20;四边形A2015B2015C2015D2015的周长$\frac{5+5\sqrt{3}}{{2}^{1006}}$.
如图,在菱形ABCD中,边长为10,∠A=60°,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是20;四边形A2015B2015C2015D2015的周长$\frac{5+5\sqrt{3}}{{2}^{1006}}$. 分析 根据菱形的性质,三角形中位线的性质以及勾股定理求出四边形各边长,得出规律求出即可.
解答 解:∵菱形ABCD中,边长为10,∠A=60°,顺次连结菱形ABCD各边中点,
∴△AA1D1是等边三角形,四边形A2B2C2D2是菱形,
∴A1D1=5,C1D1=$\frac{1}{2}$AC=5$\sqrt{3}$,A2B2=C2D2=C2B2=A2D2=5,
∴四边形A2B2C2D2的周长是:5×4=20,
同理可得出:A3D3=5×$\frac{1}{2}$,C3D3=$\frac{1}{2}$C1D1=$\frac{1}{2}$×5$\sqrt{3}$,
A5D5=5×($\frac{1}{2}$)2,C5D5=$\frac{1}{2}$C3D3=($\frac{1}{2}$)2×5$\sqrt{3}$,
…
∴四边形A2015B2015C2015D2015的周长是:$\frac{5+5\sqrt{3}}{{2}^{1006}}$
故答案为:20;$\frac{5+5\sqrt{3}}{{2}^{1006}}$.
点评 此题主要考查了菱形的性质,矩形的性质和中点四边形的性质等知识,根据已知得出边长变化规律是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | a=1 | B. | a=3 | C. | a=-2 | D. | a=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32•33=65 | B. | (2×102)(3×103)=6×106 | ||
| C. | (-xy)2•(xy)3=x5y5 | D. | (a4b)2=a4b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
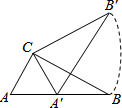 三角板∠ACB=90°,∠B=30°,BC=6,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边起始位置即停止转动,则B点转过的路径BB′的长为2π.
三角板∠ACB=90°,∠B=30°,BC=6,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边起始位置即停止转动,则B点转过的路径BB′的长为2π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com