
”¾ĢāÄæ”æÓŠĮ½øöÄŚ½Ē·Ö±šŹĒĖüĆĒ¶Ō½ĒµÄŅ»°ėµÄĖıߊĪ½Š×ö°ė¶Ō½ĒĖıߊĪ£®
£Ø1£©ČēĶ¼1£¬ŌŚ°ė¶Ō½ĒĖıߊĪABCDÖŠ£¬”ĻB£½ ![]() ”ĻD£¬”ĻC£½
”ĻD£¬”ĻC£½ ![]() ”ĻA£¬Ēó”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ£»
”ĻA£¬Ēó”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ£»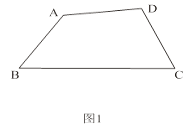
£Ø2£©ČēĶ¼2£¬Čń½Ē”÷ABCÄŚ½ÓÓŚ”ŃO£¬Čō±ßABÉĻ“ęŌŚŅ»µćD£¬Ź¹µĆBD£½BO£®”ĻOBAµÄĘ½·ÖĻß½»OAÓŚµćE£¬Į¬½įDE²¢ŃÓ³¤½»ACÓŚµćF£¬”ĻAFE£½2”ĻEAF£®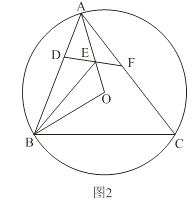
ĒóÖ¤£ŗĖıߊĪDBCFŹĒ°ė¶Ō½ĒĖıߊĪ£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬¹żµćD×÷DG”ĶOBÓŚµćH£¬½»BCÓŚµćG£®µ±DH£½BGŹ±£¬Ēó”÷BGHÓė”÷ABCµÄĆ껿֮±Č£®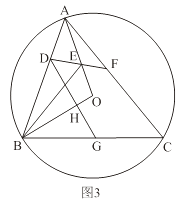
”¾“š°ø”æ
£Ø1£©
½ā£ŗŌŚ°ė¶Ō½ĒĖıߊĪABCDÖŠ£¬”ĻB=![]() ”ĻD£¬”ĻC=
”ĻD£¬”ĻC=![]() ”ĻA.
”ĻA.
”ß”ĻA+”ĻB+”ĻC+”ĻD=360”ć£¬
”ą3”ĻB+3”ĻC=360”ć.
”ą”ĻB+”ĻC=120”ć.
¼“”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ120”ć.
£Ø2£©
Ö¤Ć÷£ŗŌŚ”÷BEDŗĶ”÷BEOÖŠ£¬
 .
.
”ą”÷BED”Õ”÷BEO£ØSAS£©.
”ą”ĻBDE=”ĻBOE.
Ó֔ߔĻBCF=![]() ”ĻBOE.
”ĻBOE.
”ą”ĻBCF=![]() ”ĻBDE.
”ĻBDE.
ČēĻĀĶ¼£¬Į¬½įOC.
Éč”ĻEAF=![]() .Ōņ”ĻAFE=2”ĻEAF=2
.Ōņ”ĻAFE=2”ĻEAF=2![]() .
.
”ą”ĻEFC=180”ć-”ĻAFE=180”ć-2![]() .
.
ӧOA=OC,
”ą”ĻOAC=”ĻOCA=![]() .
.
”ą”ĻAOC=180”ć-”ĻOAC-”ĻOCA=180”ć-2![]() .
.
”ą”ĻABC=![]() ”ĻAOC=
”ĻAOC=![]() ”ĻEFC.
”ĻEFC.
”ąĖıߊĪDBCFŹĒ°ė¶Ō½ĒĖıߊĪ.

£Ø3£©
½ā£ŗČēĻĀĶ¼£¬×÷¹żµćOM”ĶBCÓŚµćM.
”ßĖıߊĪDBCFŹĒ°ė¶Ō½ĒĖıߊĪ£¬
”ą”ĻABC+”ĻACB=120”ć.
”ą”ĻBAC=60”ć.
”ą”ĻBOC=2”ĻBAC=120”ć.
ӧOB=OC
”ą”ĻOBC=”ĻOCB=30”ć.
”ąBC=2BM=![]() BO=
BO=![]() BD.
BD.
”ßDG”ĶOB,
”ą”ĻHGB=”ĻBAC=60”ć.
”ß”ĻDBG=”ĻCBA,
”ą”÷DBG![]() ”÷CBA.
”÷CBA.
”ą![]() =
=![]() 2=
2=![]() .
.
ӧDH=BG,BG=2HG.
”ąDG=3HG.
”ą![]() =
=![]()
”ą![]() =
=![]() .
.

”¾½āĪö”æ£Ø1£©ŌŚ°ė¶Ō½ĒĖıߊĪABCDÖŠ£¬”ĻB=![]() ”ĻD£¬”ĻC=
”ĻD£¬”ĻC=![]() ”ĻA£»øł¾ŻĖıߊĪµÄÄŚ½ĒŗĶĪŖ360”ć£¬µĆ³ö”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ.
”ĻA£»øł¾ŻĖıߊĪµÄÄŚ½ĒŗĶĪŖ360”ć£¬µĆ³ö”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ.
£Ø2£©ČēĶ¼Į¬½ÓOC£¬øł¾ŻĢõ¼žĻČÖ¤”÷BED”Õ”÷BEO£¬ŌŁøł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆ³ö”ĻBCF=![]() ”ĻBOE=
”ĻBOE=![]() ”ĻBDE£»Éč”ĻEAF=
”ĻBDE£»Éč”ĻEAF=![]() .Ōņ”ĻAFE=2”ĻEAF=2
.Ōņ”ĻAFE=2”ĻEAF=2![]() µĆ³ö”ĻEFC=180”ć-”ĻAFE=180”ć-2
µĆ³ö”ĻEFC=180”ć-”ĻAFE=180”ć-2![]() £»ŌŁøł¾ŻOA=OCµĆ³ö”ĻOAC=”ĻOCA=
£»ŌŁøł¾ŻOA=OCµĆ³ö”ĻOAC=”ĻOCA=![]() £¬ øł¾ŻČż½ĒŠĪÄŚ½ĒŗĶµĆ³ö”ĻAOC=180”ć-”ĻOAC-”ĻOCA=180”ć-2
£¬ øł¾ŻČż½ĒŠĪÄŚ½ĒŗĶµĆ³ö”ĻAOC=180”ć-”ĻOAC-”ĻOCA=180”ć-2![]() £»“Ó¶ųµĆÖ¤.
£»“Ó¶ųµĆÖ¤.
£Ø3£©ČēĻĀĶ¼£¬×÷¹żµćOM”ĶBCÓŚµćM£¬ÓÉĖıߊĪDBCFŹĒ°ė¶Ō½ĒĖıߊĪ£¬µĆ³ö”ĻABC+”ĻACB=120”ć£¬”ĻBAC=60”ć.”ĻBOC=2”ĻBAC=120”ć£»ŌŁÓÉOB=OC£¬µĆ³ö”ĻOBC=”ĻOCB=30”ć.BC=2BM=![]() BO=
BO=![]() BD£»øł¾Ż”÷DBG”«”÷CBAµĆ³ö“š°ø.
BD£»øł¾Ż”÷DBG”«”÷CBAµĆ³ö“š°ø.
”¾æ¼µć¾«Īö”æÕĘĪÕČż½ĒŠĪµÄÄŚ½ĒŗĶĶā½ĒŗĶµČŃüČż½ĒŠĪµÄŠŌÖŹŹĒ½ā“š±¾ĢāµÄøł±¾£¬ŠčŅŖÖŖµĄČż½ĒŠĪµÄČżøöÄŚ½ĒÖŠ£¬Ö»æÉÄÜÓŠŅ»øöÄŚ½ĒŹĒÖ±½Ē»ņ¶Ū½Ē£»Ö±½ĒČż½ĒŠĪµÄĮ½øöČń½Ē»„Óą£»Čż½ĒŠĪµÄŅ»øöĶā½ĒµČÓŚŗĶĖü²»ĻąĮŚµÄĮ½øöÄŚ½ĒµÄŗĶ£»Čż½ĒŠĪµÄŅ»øöĶā½Ē“óÓŚČĪŗĪŅ»øöŗĶĖü²»ĻąĮŚµÄÄŚ½Ē£»µČŃüČż½ĒŠĪµÄĮ½øöµ×½ĒĻąµČ£Ø¼ņ³Ę£ŗµČ±ß¶ŌµČ½Ē£©£®


 ĆæČÕ10·ÖÖÓæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
ĆæČÕ10·ÖÖÓæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘåÅĢÖŠ½ØĮ¢ČēĶ¼µÄÖ±½Ē×ų±źĻµ£¬ČżæÅĘå×ÓA£¬O£¬BµÄĪ»ÖĆČēĶ¼£¬ĖüĆĒ·Ö±šŹĒ£Ø©1£¬1£©£¬£Ø0£¬0£©ŗĶ£Ø1£¬0£©£® 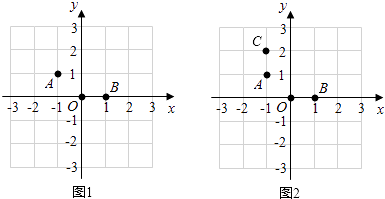
£Ø1£©ČēĶ¼2£¬Ģķ¼ÓĘå×ÓC£¬Ź¹A£¬O£¬B£¬CĖÄæÅĘå×Ó³ÉĪŖŅ»øöÖį¶Ō³ĘĶ¼ŠĪ£¬ĒėŌŚĶ¼ÖŠ»³öøĆĶ¼ŠĪµÄ¶Ō³ĘÖį£»
£Ø2£©ŌŚĘäĖūøńµćĪ»ÖĆĢķ¼ÓŅ»æÅĘå×ÓP£¬Ź¹A£¬O£¬B£¬PĖÄæÅĘå×Ó³ÉĪŖŅ»øöÖį¶Ō³ĘĶ¼ŠĪ£¬ĒėÖ±½ÓŠ“³öĘå×ÓPµÄĪ»ÖƵÄ×ų±ź£®£ØŠ“³ö2øö¼“æÉ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻ²»¶Ģ½¾æµÄĮĮĮĮĶ¬Ń§ÄĆ³öŠĪד·Ö±šŹĒ³¤·½ŠĪŗĶÕż·½ŠĪµÄĮ½æéÖ½Ę¬£¬ĘäÖŠ³¤·½ŠĪÖ½Ę¬µÄ³¤ĪŖ![]() £¬æķĪŖ
£¬æķĪŖ![]() £¬ĒŅĮ½æéÖ½Ę¬Ć껿ĻąµČ£®
£¬ĒŅĮ½æéÖ½Ę¬Ć껿ĻąµČ£®
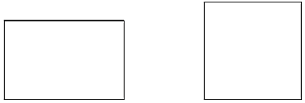
£Ø1£©ĮĮĮĮĻėÖŖµĄÕż·½ŠĪÖ½Ę¬µÄ±ß³¤£¬ĒėÄć°ļĖūĒó³öÕż·½ŠĪÖ½Ę¬µÄ±ß³¤£»£Ø½į¹ū±£ĮōøłŗÅ£©
£Ø2£©ŌŚ³¤·½ŠĪÖ½Ę¬ÉĻ½Ų³öĮ½øöĶźÕūµÄÕż·½ŠĪÖ½Ę¬£¬Ć껿·Ö±šĪŖ![]() ŗĶ
ŗĶ![]() £¬ĮĮĮĮČĻĪŖĮ½øöÕż·½ŠĪÖ½Ę¬µÄĆ껿֮ŗĶŠ”ÓŚ³¤·½ŠĪÖ½Ę¬µÄ×ÜĆ껿£¬ĖłŅŌŅ»¶ØÄܽŲ³ö·ūŗĻŅŖĒóµÄÕż·½ŠĪÖ½Ę¬Ą“£¬ÄćĶ¬ŅāĮĮĮĮµÄ¼ū½āĀš£æĪŖŹ²Ć“£æ£Ø²Īæ¼Źż¾Ż£ŗ
£¬ĮĮĮĮČĻĪŖĮ½øöÕż·½ŠĪÖ½Ę¬µÄĆ껿֮ŗĶŠ”ÓŚ³¤·½ŠĪÖ½Ę¬µÄ×ÜĆ껿£¬ĖłŅŌŅ»¶ØÄܽŲ³ö·ūŗĻŅŖĒóµÄÕż·½ŠĪÖ½Ę¬Ą“£¬ÄćĶ¬ŅāĮĮĮĮµÄ¼ū½āĀš£æĪŖŹ²Ć“£æ£Ø²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬A£Ø©2£¬2£©£¬B£Ø©3£¬©2£©
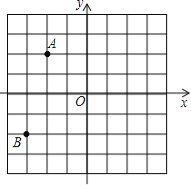
£Ø1£©ČōµćCÓėµćA¹ŲÓŚŌµćO¶Ō³Ę£¬ŌņµćCµÄ×ų±źĪŖ”” ””£»
£Ø2£©½«µćAĻņÓŅĘ½ŅĘ5øöµ„Ī»µĆµ½µćD£¬ŌņµćDµÄ×ų±źĪŖ”” ””£»
£Ø3£©ÓɵćA£¬B£¬C£¬D×é³ÉµÄĖıߊĪABCDÄŚ£Ø²»°üĄØ±ß½ē£©ČĪČ”Ņ»øöŗį”¢×Ż×ų±ź¾łĪŖÕūŹżµÄµć£¬ĒóĖłČ”µÄµćŗį”¢×Ż×ų±źÖ®ŗĶĒ”ŗĆĪŖĮćµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĢ½¾æ£ŗ
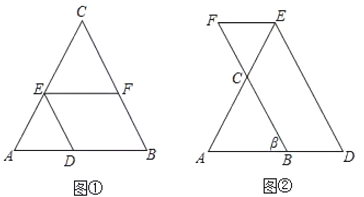
£Ø1£©ČēĶ¼¢Ł£¬ŌŚ![]() ÖŠ£¬µć
ÖŠ£¬µć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ·Ö±šŌŚ±ß
·Ö±šŌŚ±ß![]() ”¢
Ӣ![]() Ӣ
”¢![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() £¬Čō
£¬Čō![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż£®Ēė½«ĻĀĆęµÄ½ā“š¹ż³Ģ²¹³äĶźÕū£¬²¢ĢīæÕ£®
µÄ¶ČŹż£®Ēė½«ĻĀĆęµÄ½ā“š¹ż³Ģ²¹³äĶźÕū£¬²¢ĢīæÕ£®
£Ø1£©½ā£ŗ
![]() £¬
£¬
![]() £ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©£®
£ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©£®
![]() £¬
£¬
![]() £Ø___________________________________£©£®
£Ø___________________________________£©£®
![]() £Ø__________________£©£®
£Ø__________________£©£®
![]() £®
£®
Ó¦ÓĆ£ŗ
£Ø2£©ČēĶ¼¢Ś£¬ŌŚ![]() ÖŠ£¬µć
ÖŠ£¬µć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ·Ö±šŌŚ±ß
·Ö±šŌŚ±ß![]() ”¢
Ӣ![]() Ӣ
”¢![]() µÄŃÓ³¤ĻßÉĻ£¬ĒŅ
µÄŃÓ³¤ĻßÉĻ£¬ĒŅ![]() £¬
£¬![]() £¬Čō
£¬Čō£¬Ēó
![]() µÄ“󊔣®£ØÓĆŗ¬
µÄ“󊔣®£ØÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾£©£®
µÄ“śŹżŹ½±ķŹ¾£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŹĢāĒé¾³£ŗ
ĪŅĆĒÖŖµĄ£¬”°Į½ĢõĘ½ŠŠĻß±»µŚČżĢõÖ±ĻßĖł½Ų£¬Ķ¬Ī»½ĒĻąµČ£¬ÄŚ“ķ½ĒĻąµČ£¬Ķ¬ÅŌÄŚ½Ē»„²¹”±£¬ĖłŅŌŌŚÄ³Š©Ģ½¾æŠŌĪŹĢāÖŠĶعż”°¹¹ŌģĘ½ŠŠĻß”±æÉŅŌĘšµ½×Ŗ»ÆµÄ×÷ÓĆ£®
ŅŃÖŖČż½Ē°å![]() ÖŠ£¬
ÖŠ£¬![]() £¬³¤·½ŠĪ
£¬³¤·½ŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £®
£®
ĪŹĢā³õĢ½£ŗ
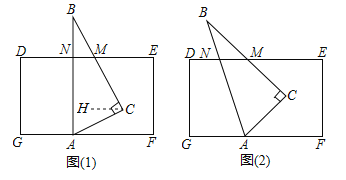
£Ø1£©ČēĶ¼£Ø1£©£¬Čō½«Čż½Ē°å![]() µÄ¶„µć
µÄ¶„µć![]() ·ÅŌŚ³¤·½ŠĪµÄ±ß
·ÅŌŚ³¤·½ŠĪµÄ±ß![]() ÉĻ£¬
ÉĻ£¬![]() Óė
Óė![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬
£¬![]() ÓŚµć
ÓŚµć![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż£®
µÄ¶ČŹż£®
¹żµć![]() ×÷
×÷![]() £¬ŌņÓŠ
£¬ŌņÓŠ![]() £¬“Ó¶ųµĆ
£¬“Ó¶ųµĆ![]() £¬“Ó¶ųæÉŅŌĒóµĆ
£¬“Ó¶ųæÉŅŌĒóµĆ![]() µÄ¶ČŹż£®
µÄ¶ČŹż£®
ÓÉ·ÖĪöµĆ£¬ĒėÄćÖ±½ÓŠ“³ö£ŗ![]() µÄ¶ČŹżĪŖ____________£¬
µÄ¶ČŹżĪŖ____________£¬![]() µÄ¶ČŹżĪŖ___________£®
µÄ¶ČŹżĪŖ___________£®
Ąą±ČŌŁĢ½£ŗ
£Ø2£©Čō½«Čż½Ē°å![]() °“Ķ¼£Ø2£©ĖłŹ¾·½Ź½°Ś·Å£Ø
°“Ķ¼£Ø2£©ĖłŹ¾·½Ź½°Ś·Å£Ø![]() Óė
Óė![]() ²»“¹Ö±£©£¬ĒėÄć²ĀĻėŠ“³ö
²»“¹Ö±£©£¬ĒėÄć²ĀĻėŠ“³ö![]() Óė
Óė![]() µÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬AB=CD£¬¶Ō½ĒĻßAC£¬BDĻą½»ÓŚµćO£¬AE”ĶBDÓŚµćE£¬CF”ĶBDÓŚµćF£¬Į¬½ÓAF£¬CE£¬ČōDE=BF£¬ŌņĻĀĮŠ½įĀŪ£ŗ¢ŁCF=AE£»¢ŚOE=OF£»¢ŪĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£»¢ÜĶ¼ÖŠ¹²ÓŠĖĶŌČ«µČČż½ĒŠĪ£®ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ

A£®4 B£®3 C£®2 D£®1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ӱŗĶŠ”ŗģĮ½Ī»Ķ¬Ń§ŌŚŃ§Ļ°”°øÅĀŹ”±Ź±£¬×öĶ¶ÖĄ÷»×Ó£ØÖŹµŲ¾łŌȵÄÕż·½Ģ壩ŹŌŃ飬ĖżĆĒ¹²×öĮĖ60“ĪŹŌŃ飬ŹŌŃéµÄ½į¹ūČēĻĀ£ŗ
³ÆÉĻµÄµćŹż | 1 | 2 | 3 | 4 | 5 | 6 |
³öĻֵēĪŹż | 7 | 9 | 6 | 8 | 20 | 10 |
£Ø1£©¼ĘĖć”°3µć³ÆÉĻ”±µÄʵĀŹŗĶ”°5µć³ÆÉĻ”±µÄʵĀŹ.
£Ø2£©Š”Ó±Ėµ£ŗ”°øł¾ŻÉĻŹöŹŌŃ飬Ņ»“ĪŹŌŃéÖŠ³öĻÖ5µć³ÆÉĻµÄøÅĀŹ×ī“ó”±£»Š”ŗģĖµ£ŗ”°Čē¹ūĶ¶ÖĄ600“Ī£¬ÄĒĆ“³öĻÖ6µć³ÆÉĻµÄ“ĪŹżÕżŗĆŹĒ100“Ī”±.Š”Ó±ŗĶŠ”ŗģµÄĖµ·ØÕżČ·Āš£æĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŅŃÖŖMN”ĶPQÓŚµćO£¬µćA”¢ ![]() ŹĒŅŌMNĪŖÖįµÄ¶Ō³Ęµć£¬¶ųµć
ŹĒŅŌMNĪŖÖįµÄ¶Ō³Ęµć£¬¶ųµć ![]() ”¢AŹĒŅŌPQĪŖÖįµÄ¶Ō³Ęµć£¬ĒóÖ¤£ŗµć
”¢AŹĒŅŌPQĪŖÖįµÄ¶Ō³Ęµć£¬ĒóÖ¤£ŗµć ![]() ”¢
”¢ ![]() ŹĒŅŌµćOĪŖ¶Ō³ĘÖŠŠÄµÄ¶Ō³Ęµć£®
ŹĒŅŌµćOĪŖ¶Ō³ĘÖŠŠÄµÄ¶Ō³Ęµć£®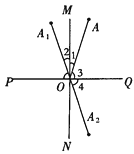
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com