
【题目】已知如图,抛物线![]() 与
与![]() 轴交于点A和点C(2,0),与
轴交于点A和点C(2,0),与![]() 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
(1)直接写出点A和点B的坐标;
(2)求![]() 和
和![]() 的值;
的值;
(3)已知点E是该抛物线的顶点,求证:AB⊥EB.
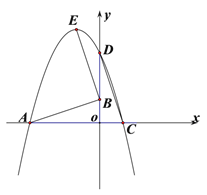
【答案】(1)A(-6,0)、B(0,2);(2)![]() ,
,![]() ;(3)E(-2,8) .
;(3)E(-2,8) .
【解析】
试题
(1)由题意易得点D的坐标为(0,6),结合AOB是由△DOC绕点O逆时针旋转90°得到的,即可得到OA=6,OB=OC=2,由此即可得到点A和点B的坐标;
(2)将点A和点C的坐标代入![]() 列出关于
列出关于![]() 的二元一次方程组,解方程组即可求得
的二元一次方程组,解方程组即可求得![]() 的值;
的值;
(3)由(2)中所得![]() 的值可得二次函数的解析式,把解析式配方即可求得点E的坐标,结合点A和点B的坐标即可求得AE2、AB2、BE2的值,这样由勾股定理的逆定理即可得到∠ABE=90°,从而可得AB⊥BE.
的值可得二次函数的解析式,把解析式配方即可求得点E的坐标,结合点A和点B的坐标即可求得AE2、AB2、BE2的值,这样由勾股定理的逆定理即可得到∠ABE=90°,从而可得AB⊥BE.
试题解析:
(1)∵在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点D的坐标为(0,6),
∵△AOB是由△DOC绕点O逆时针旋转90°得到的,
∴OA=OD=6,OB=OC=2,
∴点A的坐标为(-6,0),点B的坐标为(0,2);
(2)∵点A(-6,0)和点C(2,0)在![]() 的图象上,
的图象上,
∴![]() ,解得:
,解得: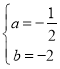 ;
;
(3)如图,连接AE,
由(2)可知![]() ,
,
∴![]() ,
,
∴点E的坐标为(-2,8),
∵点A(-6,0),点B(0,2),
∴AE2=![]() ,AB2=
,AB2=![]() ,BE2=
,BE2=![]() ,
,
∴AE2=AB2+BE2,
∴∠ABE=90°,
∴AB⊥EB.


科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一动点,
上一动点,![]() 且
且![]() ,连接
,连接![]() ,其中
,其中![]() .
.
问题发现:(1)如图1,若![]() ,
,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?直接写出答案;
的值为多少?直接写出答案;
类比探究,(2)如图2,若![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?请说明理由.
的值为多少?请说明理由.
拓展应用:(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,以
上一点,以![]() 为边,在如图所示位置作正方形
为边,在如图所示位置作正方形![]() ,点
,点![]() 为正方形
为正方形![]() 的对称中心,且
的对称中心,且![]() ,请直接写出
,请直接写出![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
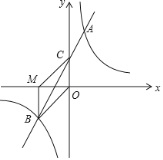
(1)求该反比例函数和一次函数的解析式;
(2)连接AO,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九年级学生的体能状况,从我校九年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A,B,C,D四个等级,请根据两幅图中的信息回答下列问题:
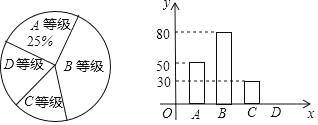
(1)求本次测试共调查了 名学生,补全条形统计图;
(2)B等级人数对应扇形统计图的圆心角的大小为 ;
(3)我校九年级共有2100名学生,请你估计九年级学生中体能测试结果为C等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
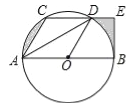
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
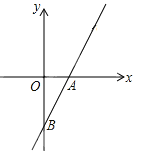
(1)求直线AB的解析式;
(2)直线AB上是否存在点C,使△BOC的面积为2?若存在,求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是反比例函数![]() 的图象,点
的图象,点![]() ,
,![]() 分别在图象的两支上,以
分别在图象的两支上,以![]() 为对角线作矩形
为对角线作矩形![]() 且
且![]() 轴.
轴.
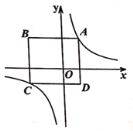
(1)当线段![]() 过原点时,分别写出
过原点时,分别写出![]() 与
与![]() ,
,![]() 与
与![]() 的一个等量关系式;
的一个等量关系式;
(2)当![]() 、
、![]() 两点在直线
两点在直线![]() 上时,求矩形
上时,求矩形![]() 的周长;
的周长;
(3)当![]() 时,探究
时,探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com