Question

已知：Rt△OAB在直角坐标系中的位置如图所示，P（3，4）为OB的中点，点C为折线OAB上的动点，线段PC把Rt△OAB分割成两部分. 问：点C在什么位置时，分割得到的三角形与Rt△OAB相似？（注：在图上画出所有符合要求的线段PC，并写出相应的点C的坐标）．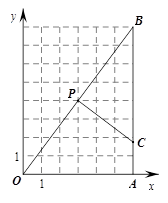

Answer 1

C₁（3，0），C₂（6，4），C₃（6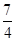，），图形见解析．

解析试题分析：按照公共锐角进行分类，可以分为两种情况：当∠BOA为公共锐角时，只存在∠PCO为直角的情况；当∠B为公共锐角时，存在∠PCB和∠BPC为直角两种情况．
试题解析：过P作PC₁⊥OA，垂足是C₁，
则△OC₁P∽△OAB．
点C₁坐标是（3，0）．
过P作PC₂⊥AB，垂足是C₂，
则△PC₂B∽△OAB．
点C₂坐标是（6，4）．
过P作PC₃⊥OB，垂足是P（如图），

则△C₃PB∽△OAB，
∴．
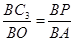易知OB=10，BP=5，BA=8，
∴．
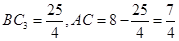∴C₃（6，）．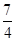
符合要求的点C有三个，其连线段分别是PC₁，PC₂，PC₃（如图）．
考点：相似变换．