
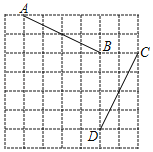
【题目】如图,在正方形网格中,![]() 、
、![]() 、
、![]() 的大小关系是______.
的大小关系是______.

【答案】![]()
【解析】
由平行线的性质可知:∠CBD=∠BDE,∠EDF=∠DFG,然后根据锐角三角形函数的定义可知:tan∠ABC=![]() ,tan∠EDF=
,tan∠EDF=![]() ,tan∠BDE=tan∠GFH=
,tan∠BDE=tan∠GFH=![]() ,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
解:如图所示:
根据图形可知:
∠CBD=∠BDE,tan∠ABC=![]()
,tan∠EDF=![]() ,
,
∴∠ABC<∠EDF
∴∠ABC+∠CBD<∠EDF+∠BDE,即∠1<∠2.
根据图形可知:∠EDF=∠DFG,tan∠BDE=![]() =
=![]() ,tan∠GFH=
,tan∠GFH=![]() ,
,
∴∠BDE=∠GFH.
∴∠EDF+∠BDE=∠DFG+∠GFH,即:∠2=∠3.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A(1,7)、B(5,5)、C(7,5)、D(5,1).
(1)将线段AB绕点B逆时针旋转,得到对应线段BE.当BE与CD第一次平行时,画出点A运动的路径,并直接写出点A运动的路径长;
(2)线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,直接写出这个旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=40°,则∠ACB=( ).

A.70°B.80°C.110°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在梯形ABCD中,AB//CD,AB=12,CD=7,点E在边AD上,![]() ,过点E作EF//AB交边BC于点F.
,过点E作EF//AB交边BC于点F.
(1)求线段EF的长;
(2)设![]() ,
,![]() ,联结AF,请用向量
,联结AF,请用向量![]() 表示向量
表示向量![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
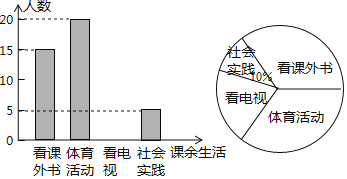
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
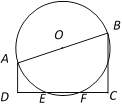
【题目】如图,梯形ABCD中,AD∥BC,∠ADC=90,AD= 2,BC= 4,![]() .以AB为直径作⊙O,交边DC于E、F两点.
.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF.
(2)求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根。
(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=![]() +
+![]() + x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
+ x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺.人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山![]() 位于树的西面.山高
位于树的西面.山高![]() 为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢
为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢![]() 恰好与山峰
恰好与山峰![]() 处在同一条直线上,人眼离地7尺.则山高
处在同一条直线上,人眼离地7尺.则山高![]() 的长为(结果保留到整数,1丈=10尺)( )
的长为(结果保留到整数,1丈=10尺)( )
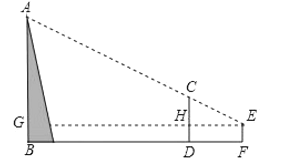
A.162丈B.163丈C.164丈D.165丈
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com