
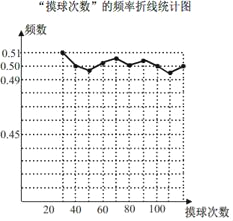
【题目】在一个不透明袋子中装有颜色不同的黑、白两种球共40个球,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.如图是“摸到白球”的频率折线统计图:
(1)根据统计图,估算盒子里黑、白两种颜色的球各多少个?
(2)如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
【答案】(1)估计盒子里白球个数约为20个,黑球个数为20个;(2)需要往盒子里再放入20个白球.
【解析】
(1)由折线统计图知,当摸球次数很大时,摸到白球的概率将会接近![]() ,所以摸到白球的概率为
,所以摸到白球的概率为![]() ,据此用球的总个数乘以白球概率可得白球数量,继而可得答案;
,据此用球的总个数乘以白球概率可得白球数量,继而可得答案;
(2)设需要往盒子里再放入![]() 个白球,根据题意得出方程,解方程即可.
个白球,根据题意得出方程,解方程即可.
(1)由折线统计图知,当摸球次数很大时,摸到白球的概率将会接近0.50,
所以摸到白球的概率为0.5,
估计盒子里白球个数约为40×0.5=20个,黑球个数为40﹣20=20个;
(2)设需要往盒子里再放入x个白球;
根据题意得:![]() =
=![]() ,
,
解得:x=20;
答:需要往盒子里再放入20个白球.


科目:初中数学 来源: 题型:
【题目】一辆自行车,前胎行驶6000km就不能继续使用,后胎行驶4000km就不能继续使用,若在行驶中合理交换前后胎,则最多可以行驶_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形且![]() ,求∠B的大小.
,求∠B的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
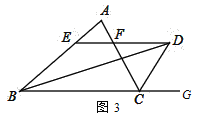
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() x2+bx﹣
x2+bx﹣![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.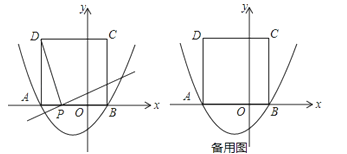
(1)b的值及点D的坐标。
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小平为了测量学校教学楼的高度,她先在A处利用测角仪测得楼顶C的仰角为30°,再向楼的方向直行50米到达B处,又测得楼顶C的仰角为60度.已知测角仪的高度是1.2米,请你帮助小平计算出学校教学楼的高度CO.(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用加法的运算律计算(+6![]() )+(-18)+(+4
)+(-18)+(+4![]() )+(-6.8)+18+(-3.2)最适当的是( )
)+(-6.8)+18+(-3.2)最适当的是( )
A. [ (+6![]() )+ (+4
)+ (+4![]() )+18]+[ (-18)+(-6.8)+(-3.2)]
)+18]+[ (-18)+(-6.8)+(-3.2)]
B. [ (+6![]() )+ (-6.8)+(+4
)+ (-6.8)+(+4![]() )]+[(-18)+18+(-3.2)]
)]+[(-18)+18+(-3.2)]
C. [ (+6![]() )+ (-18)]+[ (+4
)+ (-18)]+[ (+4![]() )+(-6.8)]+[18+(-3.2)]
)+(-6.8)]+[18+(-3.2)]
D. [ (+6![]() )+ (+4
)+ (+4![]() )]+[(-18)+18]+[(-3.2)+(-6.8)]
)]+[(-18)+18]+[(-3.2)+(-6.8)]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com