
分析 (1)分析同向与背向而行,两者之间路程的关系,由此即可得出结论;
(2)设小红的速度为xm/s,爷爷的速度为ym/s,根据(1)中的等量关系,即可得出关于x、y的二元一次方程组,解之即可得出结论.
解答 解:(1)小红走200s的路程-爷爷走200s的路程=400米;
小红走40s的路程+爷爷走40s的路程=400米;
(2)设小红的速度为xm/s,爷爷的速度为ym/s.
根据题意得:$\left\{\begin{array}{l}{200x-200y=400}\\{40x+40y=400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$.
答:小红的跑步速度为6m/s,爷爷的跑步速度为4m/s.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)分同向与背向而行,找出等量关系;(2)根据等量关系,列出二元一次方程组.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a-3(a≠0)的顶点为A.
在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a-3(a≠0)的顶点为A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.
星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
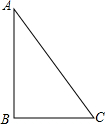 如图,Rt△ABC中,∠B=90°,AB=3,AC=5.
如图,Rt△ABC中,∠B=90°,AB=3,AC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
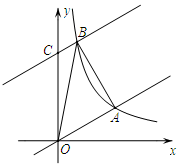 如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).
如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com