
【题目】如图,O是坐标原点,直线OA与双曲线![]() 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=![]() .
.
(1)求双曲线的解析式;
(2)直线AC与y轴交于点C(0,1),与x轴交于点D,求D点的坐标.

【答案】(1)![]() ; (2)D(-4,0)
; (2)D(-4,0)
【解析】试题分析:(1)根据正切的定义得到![]() ,而OB=4,得到AB=2,则A点坐标为(4,2),然后把A(4,2)代入
,而OB=4,得到AB=2,则A点坐标为(4,2),然后把A(4,2)代入![]() 即可求出k,从而确定双曲线的解析式;
即可求出k,从而确定双曲线的解析式;
(2)先利用待定系数法求出直线AC的解析式,然后确定D点坐标.
试题解析:解:(1)∵AB⊥x轴,OB=4,tan∠AOB=![]() ,∴
,∴![]() ,∴AB=2,∴A点坐标为(4,2),把A(4,2)代入
,∴AB=2,∴A点坐标为(4,2),把A(4,2)代入![]() 得,k=4×2=8,∴双曲线的解析式为
得,k=4×2=8,∴双曲线的解析式为![]() ;
;
(2)设直线AC的解析式为y=kx+b,把A(4,2)、C(0,1)代入得,4k+b=2,b=1,解得k=![]() ,b=1,∴直线AC的解析式为y=
,b=1,∴直线AC的解析式为y=![]() x+1,令y=0,则
x+1,令y=0,则![]() x+1=0,解得x=﹣4,∴D点坐标为(﹣4,0).
x+1=0,解得x=﹣4,∴D点坐标为(﹣4,0).


科目:初中数学 来源: 题型:
【题目】2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐篷;
(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新罗区中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要5.5万元,购买2台电脑和1台电子白板需要5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过50万元,则最多能购买电子白板多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.

(1)该顾客最少可得_________元购物券,最多可得_________元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
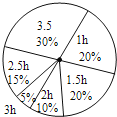
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com