
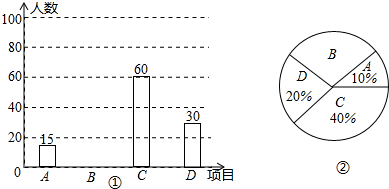
分析 (1)用A的人数除以所占的百分比,即可求出调查的学生数;
(2)用抽查的总人数减去A、C、D的人数,求出喜欢“立定跳远”的学生人数,再除以被调查的学生数,求出所占的百分比,再画图即可;
(3)用A表示男生,B表示女生,画出树形图,再根据概率公式进行计算即可.
解答 解:(1)根据题意,得:15÷10%=150(人),
答:在这项调查中,共调查了150名学生;
(2)本次调查中喜欢“立定跳远”的学生人数为:150-15-60-30=45(人),
“立定跳远”的学生占被调查学生百分比为:$\frac{45}{150}$×100%=30%,
补全图形如下: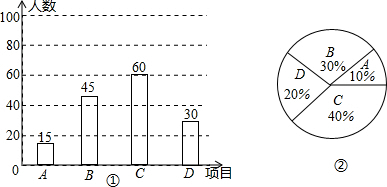
(3)用A表示男生,B表示女生,画图如下:
共有20种情况,同性别学生的情况是8种,
则刚好抽到同性别学生的概率是$\frac{8}{20}$=$\frac{2}{5}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用以及概率的求法,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
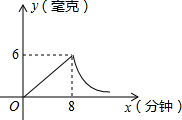 为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:
为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
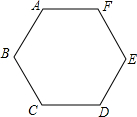 如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.
如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.
已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
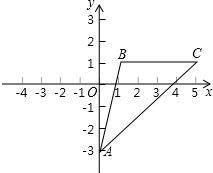 在平面直角坐标系中,已知点A(0,-3),点B(m,1),C(m+4,1);
在平面直角坐标系中,已知点A(0,-3),点B(m,1),C(m+4,1);查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 移植总数(n) | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
| 成活数(m) | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
| 成活的频率$\frac{m}{n}$ | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com