
【题目】如图,在平面直角坐标系中,已知△ABC,∠ABC=90°,顶点A在第一象限,B、C在x轴的正半轴上(C在B的右侧),BC=3,AB=4,若双曲线![]() 交边AB于点E,交边AC于中点D.
交边AB于点E,交边AC于中点D.
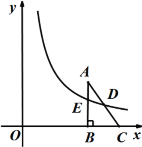
(1)若OB=2,求k;
(2)若AE=![]() , 求直线AC的解析式.
, 求直线AC的解析式.
【答案】(1)7;(2)y=-![]() x+12.
x+12.
【解析】
(1)过D作BC垂线,根据D为中点,得到D点坐标,代入可求得结果;
(2)设OB为a,E,D点坐标为关于a的代数式,代入函数可求得a值,继而可得到A,C点坐标,根据已知直线上两点,求直线解析式,即可求得AC解析式.
(1)如图,
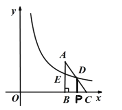
过D作BC垂线,交BC于P点,
∵BC=3,D为AC中点,
∴BP=![]() BC=
BC=![]() ,
,
∵OB=2,∴OP=![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0)
,0)
∵AB=4,∴D点坐标为(![]() ,2),
,2),
∵D在y=![]() 上,代入D点坐标,
上,代入D点坐标,
∴k=7;
故答案为7;
(2)∵AE=![]() AB=
AB=![]() ×4=
×4=![]() ,
,
∴BE=AB-AE=4-![]() =
=![]() ,
,
设OB=a,则E点坐标为(a,![]() ),D点坐标为(a+
),D点坐标为(a+![]() ,2),
,2),
∵D,E在y=![]() 上,
上,
∴k=xy=![]() a=2(a+
a=2(a+![]() ),
),
∴a=6,
∴A点坐标为(6,4),C点坐标为(9,0),
设AC的解析式为y=kx+b,A,C坐标代入,
求得k=-![]() ,b=12,
,b=12,
故AC的解析式为y=-![]() x+12.
x+12.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=5,BC=12.如果分别以A、C为圆心的两圆外切,且圆A与直线BC相交,点D在圆A外,那么圆C的半径长r的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数![]() 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为![]() ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 1 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
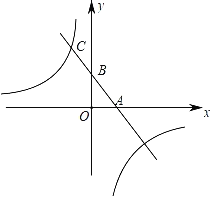
【题目】如图,在平面直角坐标系xOy中,直线y=kx+3与x,y轴分别交于点A、B,与双曲线y=![]() 交于点C(a,6),已知△AOB的面积为3,求直线与双曲线的表达式.
交于点C(a,6),已知△AOB的面积为3,求直线与双曲线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
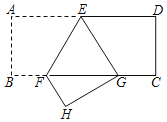
【题目】如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
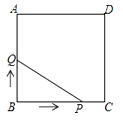
【题目】如图,正方形![]() 的边长为
的边长为![]() ,动点
,动点![]() 从
从![]() 点出发,以
点出发,以![]() 的速度沿着边
的速度沿着边![]() 运动,到达
运动,到达![]() 点停止运动;另一动点
点停止运动;另一动点![]() 同时从
同时从![]() 点出发,以
点出发,以![]() 的速度沿着边
的速度沿着边![]() 向
向![]() 点运动,到达
点运动,到达![]() 点停止运动.设
点停止运动.设![]() 点的运动时间为
点的运动时间为![]() 单位:
单位:![]() ,
,![]() 的面积为
的面积为![]() 单位:
单位:![]() ,则
,则![]() 与
与![]() 的函数关系的大致图象为( )
的函数关系的大致图象为( )
A. 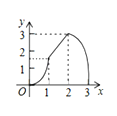 B.
B.  C.
C. 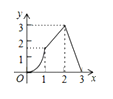 D.
D. 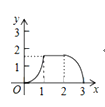
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动支付快捷高效,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种,移动支付支付方式,为此在某步行街,使用某app,软件对使用移动支付的行人进行随机抽样调查,设置了四个选项,支付宝,微信,银行卡,其他移动支付(每人只选一项),以下是根据调查结果分别整理的不完整的条形统计图和扇形统计图.
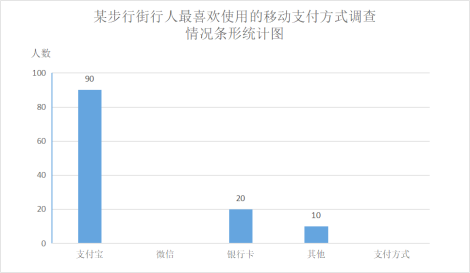

请你根据下列统计图提供的信息,完成下列问题.
(1)这次调查的样本容量是 ;
(2)请补全条形统计图;
(3)求在此次调查中表示使用微信支付的扇形所对的圆心角的度数.
(4)若某天该步行街人流量为10万人,其中40%的人购物并选择移动支付,请你依据此次调查获得的信息,估计一下当天使用银行卡支付的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
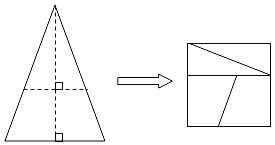
【题目】如图,将等腰三角形纸片沿图中虚线剪成四块图形,用这四块图形进行拼接,恰能拼成一个没有缝隙的正方形,则正方形的边长与等腰三角形的底边长的比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
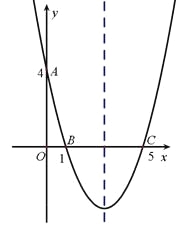
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com