
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
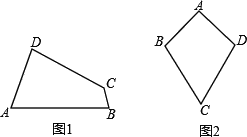
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=78°,∠B=82°,则∠C=_________,∠D=__________
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例(提示:举反例可画图并说明)
(3)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=![]() ,AD=
,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
【答案】(1)118°,82°;(2)①见解析,②小红的猜想不正确,反例见解析;(3)AC的长为![]() 或
或![]()
【解析】
(1)根据四边形ABCD是“等对角四边形”得出∠D=∠B=82°,根据多边形内角和定理求出∠C即可;
(2)①连接BD,根据等边对等角得出∠ABD=∠ADB,求出∠CBD=∠CDB,根据等腰三角形的判定得出即可;
②不正确.举一个使其结论不成立的反例即可.
(3)分两种情况讨论:当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,利用勾股定理求解;当∠BCD=∠DAB=60°时,过点D作DE⊥AB于点E,DF⊥BC于点F,求出线段利用勾股定理求解.
(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠B=82°,
∴∠D=∠B=82°
∴∠C=360°-∠A-∠B-∠D=118°
故答案为:118°,82°
(2)①如图,连接BD,

∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴∠CBD=∠CDB,
∴CB=CD;
②小红的猜想不正确,如图:
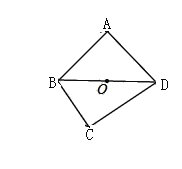
四边形ABCD是“等对角四边形”∠A=∠C=90°,AB=AD,但![]() ,
,
所以小红的猜想不正确;
(3)分两种情况:
①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,如图:
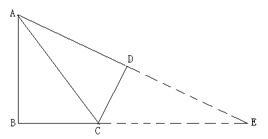
∵∠ABC=90°,∠DAB=60°,AB=![]() ,
,
∴∠E=30°,
∴AE=2AB=![]() ,
,
∴DE=AE﹣AD=![]() ,
,
∵∠EDC=90°,∠E=30°,
∴CD=![]() 6,
6,
∴AC=![]() =
=![]() ;
;
②当∠BCD=∠DAB=60°时,
过点D作DM⊥AB于点M,DN⊥BC于点N,如图:
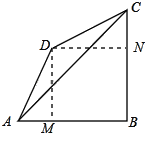
则∠AMD=90°,四边形BNDM是矩形,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM=![]() AD=
AD=![]() ,
,
∴DM=![]() 6
6
∴BM=AB﹣AM=![]() ,
,
∵四边形BNDM是矩形,
∴DN=BM=![]() ,BN=DM=6,
,BN=DM=6,
∵∠BCD=60°,
∴CN=![]() 3,
3,
∴BC=CN+BN=9,
∴AC=![]()
![]() ;
;
综上所述:AC的长为![]() 或
或![]()
![]()


科目:初中数学 来源: 题型:
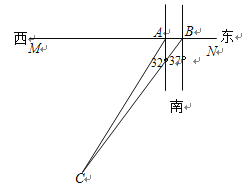
【题目】如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°= cot53°≈0.755,cot37°= tan53°≈1.327,tan32°= cot58°≈0.625,cot32°= tan58°≈1.600.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
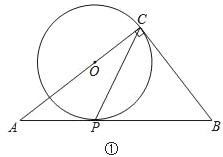
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
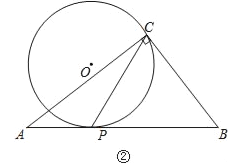
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
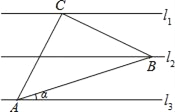
【题目】如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角三角形ABC的直角顶点C在l1上,另两个顶点A,B分别在l3,l2上,则sinα的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
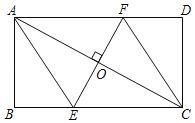
【题目】过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=6,AC=10,EC=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市为创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶(如图所示),据调查该城市的A、B、C三个社区积极响应号并购买,具体购买的数和总价如表所示.
社区 | 甲型垃圾桶 | 乙型垃圾桶 | 总价 |
A | 10 | 8 | 3320 |
B | 5 | 9 | 2860 |
C | a | b | 2820 |
(1)运用本学期所学知识,列二元一次方程组求甲型垃圾桶、乙型垃圾桶的单价每套分别是多少元?
(2)按要求各个社区两种类型的垃圾桶都要有,则a= .

查看答案和解析>>
科目:初中数学 来源: 题型:
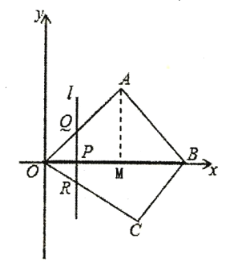
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 在第一象限,点
在第一象限,点![]() 在第四象限,点
在第四象限,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.![]() 且
且![]() ,
,![]() ,
,![]() 的长分别是二元一次方程组
的长分别是二元一次方程组![]() 的解(
的解(![]() ).
).
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,交边
,交边![]() 或边
或边![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() .已知
.已知![]() 时,直线
时,直线![]() 恰好过点
恰好过点![]() .
.
①当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②当![]() 时,求点
时,求点![]() 的横坐标
的横坐标![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com