【题目】如图所示，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．
科目：初中数学 来源： 题型：
【题目】某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的
少10人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：
（1）报两门课的共有多少人？
（2）调动后，报名第一门课的人数为 人，第二门课人数为 人．
（3）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，每个小正方形边长为1，点A的坐标为(－2，3)、点B的坐标为(－3，1)、点C的坐标为(1，-2)
(1)作出△ABC关于y轴对称的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点，不写画法）.
(2) 直接写出A′、B′、C三点的坐标.
(3)在x轴上求作一点P，使PA+PB的值最小.（简要写出作图步骤）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知,如图, AB∥CD，∠1=∠2，那么∠E和∠F相等吗? 为什么?
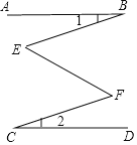
【答案】相等，理由见解析.
【解析】试题分析：分别过E、F 点作CD的平行线EM、FN，根据平行线的性质得CD∥FN∥EM∥AB，则∠3=∠1，∠4=∠5，∠1=∠6，而∠1=∠2，于是3+∠4=∠5+∠6．
试题解析：分别过E、F 点作CD的平行线EM、FN，如图
∵AB∥CD，
∴CD∥FN∥EM∥AB，
∴∠3=∠2，∠4=∠5，∠1=∠6，
而∠1=∠2，
∴∠3+∠4=∠5+∠6，
即∠BEF=∠EFC．
【题型】解答题
【结束】
26
【题目】(1)填空21－20＝2( )； 22－21＝2( ) ；23 －22＝2( )
(2)请用字母表示第n个等式，并验证你的发现．
(3)利用(2)中你的发现，求20＋21＋22＋23＋…＋22016＋22017的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】种植草莓大户张华现有22吨草莓等待出售，有两种销售渠道，一是运往省城直接批发给零售商，二是在本地市场零售，受客观因素影响，张华每天只能采用一种销售渠道，而且草莓必须在10天内售出（含10天）经过调查分析，这两种销售渠道每天销量及每吨所获纯利润见右表：
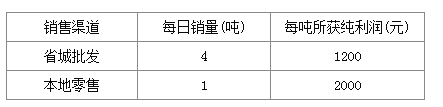
（1）若一部分草莓运往省城批发给零售商，其余在本地市场零售，请写出销售22吨草莓所获纯利润y（元）与运往省城直接批发零售商的草莓量x（吨）之间的函数关系式；
（2）怎样安排这22吨草莓的销售渠道，才使张华所获纯利润最大？并求出最大纯利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中．点E，F分别在BC，CD上，△AEF是等边三角形．连接AC交EF于点G．过点G作GH⊥CE于点H．若
，则
=（ ）
A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学七（2）班学生去劳动实践基地开展实践劳动，在劳动前需要分成x组，若每组11人，则余下一人，若每组12人，则有一组少4人，若每组分配7人，则该班可分成_____组．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=40°，则下列结论：
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正确的结论有_______________（填结论前面的序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程（x-3）(x-2)-p2=0.
（1）求证：无论p取何值时，方程总有两个不相等的实数根；
（2）设方程两实数根分别为x1、x2，且满足x12+x22=3 x1x2，求实数p的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
