
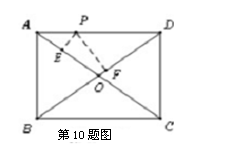
 中,
中, 为
为 上一点,且
上一点,且 .
. 为等腰直角三角形,斜边
为等腰直角三角形,斜边 与
与 交于点
交于点 ,延长
,延长 与
与 的延长线交于点
的延长线交于点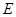 ,连接
,连接 、
、 ,作
,作 ,垂足为
,垂足为 ,下列结论:①
,下列结论:① ≌
≌ ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ ;⑤
;⑤ .其中正确的个数为( )
.其中正确的个数为( )
| A.2个 | B.3个 | C.4个 | D.5个 |
 BC,设AB=BC=3x,则MG=MC+CG=BC=3x,CG=NG=x,由NG∥AB得△EGN∽△EBA,利用相似比证明MG≠EG即可;④分别求两个三角形的底和高,再比较面积;⑤利用旋转法将△AMB绕A点逆时针旋转90°到△AHD的位置,证明△AHF≌△AMF即可.
BC,设AB=BC=3x,则MG=MC+CG=BC=3x,CG=NG=x,由NG∥AB得△EGN∽△EBA,利用相似比证明MG≠EG即可;④分别求两个三角形的底和高,再比较面积;⑤利用旋转法将△AMB绕A点逆时针旋转90°到△AHD的位置,证明△AHF≌△AMF即可.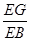 =
=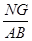 =
= ,EG=
,EG= BG=2x,MG≠EG,故MN≠EN,错误;
BG=2x,MG≠EG,故MN≠EN,错误;


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:不详 题型:解答题
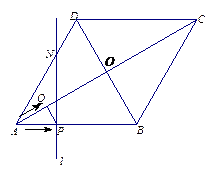
 否存在这样的t,使得△PMN是以PN为一直角边的
否存在这样的t,使得△PMN是以PN为一直角边的 直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 沿
沿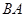 方向平移得到梯形
方向平移得到梯形 ,
, 与
与 相交于点
相交于点 ,
, =20cm,
=20cm, =5cm,
=5cm, =4cm,图中阴影部分的面积与哪个四边形的面积相等,并求出阴影部分的面积
=4cm,图中阴影部分的面积与哪个四边形的面积相等,并求出阴影部分的面积
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
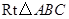 中,
中, ,
, ,
, 两点分别在
两点分别在 上,
上, ,
,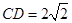 ,将
,将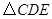 绕点
绕点 顺时针旋转,得到
顺时针旋转,得到 (如图4,点
(如图4,点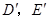 分别与
分别与 对应),点
对应),点 在
在 上,
上, 与
与 相交于点
相交于点 .
.
 的度数;
的度数; 是梯形;
是梯形; 的面积.
的面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,AB=3,CD=6,BE⊥BC交直线AD于点E.
,AB=3,CD=6,BE⊥BC交直线AD于点E. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com