
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
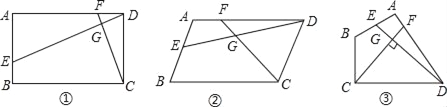
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且ADDF=AEDC,求证:DE⊥CF:
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DECD=CFDA:
(3)如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断![]() 是否为定值,并证明.
是否为定值,并证明.
【答案】(1)证明见解析 (2)证明见解析 (3)答案见解析
【解析】
(1)根据已知条件得到四边形ABCD是矩形,由矩形的性质得到∠A=∠FDC=90°,根据相似三角形的性质得到∠CFD=∠AED,根据余角的性质即可得到结论;
(2)根据已知条件得到△DFG∽△DEA,推出![]() ,根据△CGD∽△CDF,得到
,根据△CGD∽△CDF,得到
![]() ,等量代换即可得到结论;
,等量代换即可得到结论;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出![]() ,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,解方程得到CN,证出△AED∽△NFC,即可得出答案.
,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,解方程得到CN,证出△AED∽△NFC,即可得出答案.
(1)证明:∵AB∥CD,AB=CD,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵ADDF=AEDC,
∴![]()
∴△AED∽△DFC,
∴∠CFD=∠AED,
∵∠ADE+∠AED=90°,
∴∠ADE+∠CFD=90°,
∴∠DGF=90°,
∴DE⊥CF;
(2)证明:∵∠A=∠EGC,∠ADE=∠GDF,
∴△DFG∽△DEA,
∴![]()
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠AED=∠EDC,
∴∠B=∠ADC,
∵△DFG∽△DEA,
∴∠AED=∠DFG,
∴DFC=∠GDC,
∵∠DCG=∠FCD,
∴△CGD∽△CDF,
∴![]()
∴![]() ,
,
∴DECD=CFDA;
(3)解:![]() 为定值,
为定值,
理由:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中,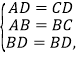
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() ,
,
∴![]()
∴![]()
在Rt△CMB中,![]() ,BM=AM﹣AB=x﹣3,由勾股定理得:BM2+CM2=BC2,
,BM=AM﹣AB=x﹣3,由勾股定理得:BM2+CM2=BC2,
∴![]()
x=0(舍去),![]()
∴![]()
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴![]()


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
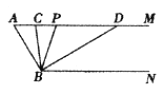
【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=12,点M、N是线段AB上的两点,且AM=BN=2,点P是线段MN上的动点,分别以线段AP、BP为边在AB的同侧作正方形APDC、正方形PBFE,点G、H分别是CD、EF的中点,点O是GH的中点,当P点从M点到N点运动过程中,OM+OB的最小值是( )

A.10B.12C.2 ![]() D.12
D.12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-20)+(+3)+(-5)+(+7);
(2)16-(-15)-4+(-5);
(3)(-12)×(-37)×![]() ;
;
(4)(-![]() )÷
)÷![]() ÷(-
÷(-![]() );
);
(5)-30×(![]()
![]()
![]() );
);
(6)-3-[-5 +(1-![]() ×0.6)÷(-3)]
×0.6)÷(-3)]
(7)![]()
(8)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 y=![]() 的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
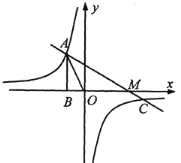
(1)求a、k的值;
(2)若一次函数y=mx+n图像经过点A和反比例函数图像上另一点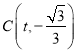 ,且与x轴交于M点,求AM的值:
,且与x轴交于M点,求AM的值:
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在一次数函数y=bx上,则b= ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
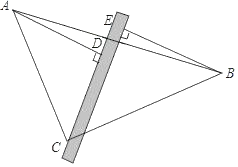
【题目】将含有45°角的直角三角板ABC和直尺如图摆放在桌子上,然后分别过A、B两个顶点向直尺作两条垂线段AD,BE.
(1)请写出图中的一对全等三角形并证明;
(2)你能发现并证明线段AD,BE,DE之间的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
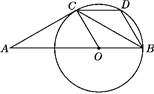
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com