
【题目】在一次羽毛球赛中,甲运动员在离地面![]() 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).

(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
【答案】(1)y=﹣![]() (x﹣5)2+3;(2)CN=3
(x﹣5)2+3;(2)CN=3![]() ﹣1(米);(3)m的取值范围为:6<m<8.
﹣1(米);(3)m的取值范围为:6<m<8.
【解析】
(1)设抛物线解析式为y=a(x5)2+3,将点(0,![]() )代入可得出a的值,继而得出抛物线解析式;
)代入可得出a的值,继而得出抛物线解析式;
(2)令y=0,可得出ON的长度,由NC=ONOC即可得出答案;
(3)先计算出刚好接到球时m的值,从而结合所给图形可得出运动员接球高度不够m的取值范围.
(1)设抛物线解析式为y=a(x﹣5)2+3,
将点(0,![]() )代入可得:
)代入可得:![]() =a(0﹣5)2+3,
=a(0﹣5)2+3,
解得:a=﹣![]() ,
,
故抛物线的解析式为:y=﹣![]() (x﹣5)2+3;
(x﹣5)2+3;
(2)当y=0时,﹣![]() (x﹣5)2+3=0,
(x﹣5)2+3=0,
解得:x1=5﹣3![]() (舍去),x2=5+3
(舍去),x2=5+3![]() ,
,
即ON=5+3![]() ,
,
∵OC=6,
∴CN=3![]() ﹣1(米);
﹣1(米);
(3)若运动员乙原地起跳到最大高度时刚好接到球,
此时﹣![]() (m﹣5)2+3=2.4,
(m﹣5)2+3=2.4,
解得:m1=2,m2=8,
∵运动员接球高度不够,
∴2<m<8,
∵OC=6,乙运动员接球时不能触网,
∴m的取值范围为:6<m<8.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
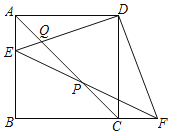
【题目】如图,在边长为4的正方形ABCD中,∠EDF=90°,点E在边AB上且不与点A重合,点F在边BC的延长线上,DE交AC于Q,连接EF交AC于P
(1)求证:△ADE≌△CDF;
(2)求证:PE=PF;
(3)当AE=1时,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
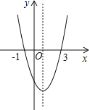
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
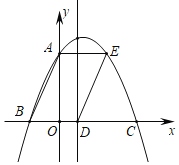
【题目】如图,抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
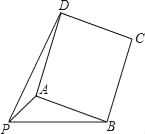
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
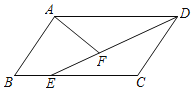
【题目】如图,在平行四边形ABCD中,E为BC边上一点,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证△ADF∽△DEC;
(2)若BE=2,AD=6,且DF=![]() DE,求DF的长度.
DE,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
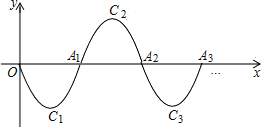
A.0B.﹣![]() C.2D.﹣2
C.2D.﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com