
【题目】如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

A.12B.9C.6D.3
【答案】D
【解析】
根据题意,作点P关于OA、OB的对称点E、D,连接DE,与OA相交于点M,与OB相交于点N,则此时△PMN周长的最小值是线段DE的长度,连接OD、OE,由∠AOB=30°,得到∠DOE=60°,由垂直平分线的性质,得到OD=OE=OP=3,则△ODE是等边三角形,即可得到DE的长度.
解:如图:作点P关于OA、OB的对称点E、D,连接DE,与OA相交于点M,与OB相交于点N,则此时△PMN周长的最小值是线段DE的长度,连接OD、OE,
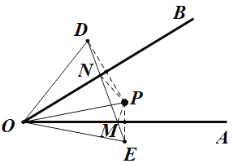
由垂直平分线的性质,得DN=PN,MP=ME,OD=OE=OP=3,
∴△PMN周长的最小值是:PN+PM+MN=DN+MN+ME=DE,
由垂直平分线的性质,得∠DON=∠PON,∠POM=∠EOM,
∴∠DOE=∠DOP+∠EOP=2(∠PON+∠POM)=2∠MON=60°,
∴△ODE是等边三角形,
∴DE=OD=OE=3,
∴△PMN周长的最小值是:PN+PM+MN=DE=3;
故选:D.


科目:初中数学 来源: 题型:
【题目】(发现)任意三个连续偶数的平方和是4的倍数。
(验证)(1)![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续偶数的中间一个为![]() ,写出它们的平方和,并说明是4的倍数。
,写出它们的平方和,并说明是4的倍数。
(延伸)(3)设三个连续奇数的中间一个数为![]() ,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少?
,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A点的坐标为(1,0).以OA为边在x轴上方画一个正方形OABC.以原点O为圆心,正方形的对角线OB长为半径画弧,与x轴正半轴交于点D.

(1)点D的坐标是 ;
(2)点P(x,y),其中x,y满足2x-y=-4.
①若点P在第三象限,且△OPD的面积为3![]() ,求点P的坐标;
,求点P的坐标;
②若点P在第二象限,判断点E(![]() +1,0)是否在线段OD上,并说明理由.
+1,0)是否在线段OD上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,幵始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程![]() 关于时间
关于时间![]() 的图象,那么符合小明行驶情况的大致图象是( )
的图象,那么符合小明行驶情况的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
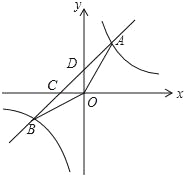
【题目】如图,点A(m,4),B(﹣4,n)在反比例函数y=![]() (k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(1)若m=2,求n的值;
(2)求m+n的值;
(3)连接OA、OB,若tan∠AOD+tan∠BOC=1,求直线AB的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了轴对称知识之后,数学兴趣小组的同学们对课本习题进行了深入研究,请你跟随兴趣小组的同学,一起完成下列问题.
(1)(课本习题)如图①,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD. 求证:DB=DE
(2)(尝试变式)如图②,△ABC是等边三角形,D是AC边上任意一点,延长BC至E,使CE=AD.
求证:DB=DE.
(3)(拓展延伸)如图③,△ABC是等边三角形,D是AC延长线上任意一点,延长BC至E,使CE=AD请问DB与DE是否相等? 并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着气温的升高,空调的需求量大增,某家电超市对每台进价分别为![]() 元、
元、![]() 元的
元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:

(1)求![]() 、
、![]() 两种型号空调的售价;
两种型号空调的售价;
(2)若该家电超市准备与不多于![]() 元的资金,采购这两种型号的空调
元的资金,采购这两种型号的空调![]() 台,求
台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这![]() 台空调能否山实现利润不低于
台空调能否山实现利润不低于![]() 元的目标?若能,请给出采购方案.若不能,请说明理由.
元的目标?若能,请给出采购方案.若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com