
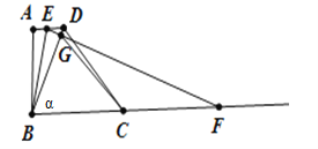
【题目】如图,在四边形ABCD中AD∥BC,∠A=90°,AB=6,BC=10,点E为边AD上一点,将ABE沿BE翻折,点A落在对角线BD上的点G处,连接EG并延长交射线BC于点F.
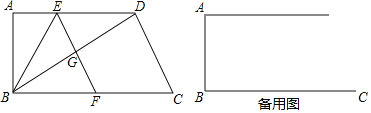
(1)如果cos∠DBC![]() ,求EF的长;
,求EF的长;
(2)当点F在边BC上时,连接AG,设AD=x,![]() y,求y关于x的函数关系式并写出x的取值范围;
y,求y关于x的函数关系式并写出x的取值范围;
(3)连接CG,如果△FCG是等腰三角形,求AD的长.
【答案】(1)EF=9;(2)y![]() (x
(x![]() );(3)AD的长为
);(3)AD的长为![]() 或
或![]()
【解析】
(1)利用S△BEF=![]() BFAB=
BFAB=![]() EFBG,即可求解;
EFBG,即可求解;
(2)过点A作AH⊥BG交于点H,连接AG,设:BF=a,先表示出AH,根据三角形面积公式可得y![]() ,由tanα
,由tanα![]() 可得a2=36+(
可得a2=36+(![]() )2,整理可得y关于x的函数关系式,根据BF≤10可求出x的取值范围.
)2,整理可得y关于x的函数关系式,根据BF≤10可求出x的取值范围.
(3)分GF=FC、CF=CG两种情况,求解即可.
(1)将△ABE沿BE翻折,点A落在对角线BD上的点G处,
∴BG⊥EF,BG=AB=6,
cos∠DBC![]() ,则:BF=9,
,则:BF=9,
S△BEF![]() BFAB
BFAB![]() EFBG,即:9×6=6×EF,
EFBG,即:9×6=6×EF,
则EF=9;
(2)过点A作AH⊥BG交于点H,连接AG,设:BF=a,
在Rt△BGF中, cosα![]() ,则tanα
,则tanα![]() ,
,
∵∠BAH+∠ABH=90°,∠ADB+∠ABH=90°,
∴∠BAH=∠ADB= a,
∴AH=6cos a,
∴y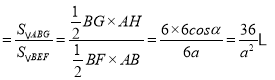 ①,
①,
∵tanα![]() ,
,
∴a2=36+(![]() )2…②,
)2…②,
把②式代入①式整理得:y![]() ;
;
∵BF≤10,
∴36+(![]() )2≤100,
)2≤100,
解之得x![]() ,
,
∴y![]() (x
(x![]() );
);
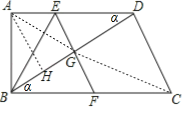
(3)①当GF=FC时,
∵cosα![]() ,
,
∴![]() ,
,
∴BF=![]() ,
,
∴FC=10-![]() ,
,
∵sinα=![]() ,
,
∴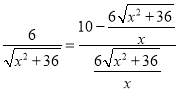 ,
,
整理得,
4x2-45x=0,
∴x1![]() ,x2=0(舍去),
,x2=0(舍去),
∴AD![]() ;
;
②当CF=CG时,
∵CF=CG,
∴∠CFG=∠CGF,
∵∠CFG+∠CBG=90°,∠CGF+∠CGB=90°,
∴∠CBG=∠CGB,
∴CG=CB=CF=10,
∴BF=20.
∵sinα=![]() ,
,
∴![]() ,
,
整理得
91x2=324,
∴x1![]() ,x2
,x2![]() (舍去);
(舍去);
故:AD的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为___________.

【答案】x>1
【解析】分析:题目要求 kx+b>0,即一次函数的图像在x 轴上方时,观察图象即可得x的取值范围.
详解:
∵kx+b>0,
∴一次函数的图像在x 轴上方时,
∴x的取值范围为:x>1.
故答案为:x>1.
点睛:本题考查了一次函数与一元一次不等式的关系,主要考查学生的观察视图能力.
【题型】填空题
【结束】
16
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
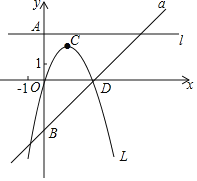
(1)若AB=8,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
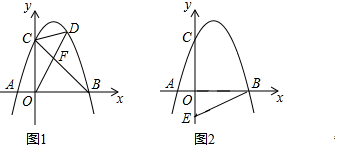
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
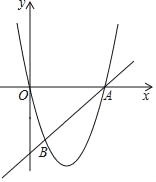
【题目】如图,在平面直角坐标系xOy中,直线AB与抛物线y=ax2+bx交于点A(6,0)和点B(1,﹣5).
(1)求这条抛物线的表达式和直线AB的表达式;
(2)如果点C在直线AB上,且∠BOC的正切值是![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
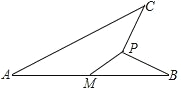
【题目】如图,线段 AB=4,M 为 AB 的中点,动点 P 到点 M 的距离是 1,连接 PB,线段
PB 绕点 P 逆时针旋转 90°得到线段 PC,连接 AC,则线段 AC 长度的最大值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
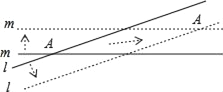
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com