
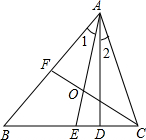
 如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.
如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
| 等 级 | A | B | C |
| 票价(元/张) | 未知 | 未知 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:
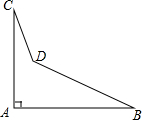 一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.
一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com