
 如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3.点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE,当点D在边BC上运动时,OE的长度的最小值是多少?
如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3.点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE,当点D在边BC上运动时,OE的长度的最小值是多少? 分析 过点D作DG⊥OA,过点E作HE⊥DG.先证明△HED≌△GDA,从而得到HE=DG=3,HD=AG.设D(a,3),则DC=a,DH=AG=4-a,则E(a+3,7-a),依据两点间的距离公式可得到OE=$\sqrt{(a+3)^{2}+(7-a)^{2}}$,最后利用配方法求得被开方数的最小值即可.
解答 解:如图所示:过点D作DG⊥OA,过点E作HE⊥DG.
∵DG⊥OA,HE⊥DG,
∴∠EHD=∠DGA=90°.
∴∠GDA+∠DAG=90°.
∵四边形ADEF为正方形,
∴DE=AD,∠HDE+∠GDA=90°.
∴∠HDE=∠GAD.
在△HED和△GDA中$\left\{\begin{array}{l}{∠HDE=∠GAD}\\{∠EHD=∠DGA}\\{DE=AD}\end{array}\right.$,
∴△HED≌△GDA.
∴HE=DG=3,HD=AG.
设D(a,3),则DC=a,DH=AG=4-a.
∴E(a+3,7-a).
∴OE=$\sqrt{(a+3)^{2}+(7-a)^{2}}$=$\sqrt{2(a-2)^{2}+50}$.
当a=2时,OE有最小值,最小值为5$\sqrt{2}$.
点评 本题主要考查的是正方形的性质、二次函数的最值、全等三角形的性质和判定,得到点E的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
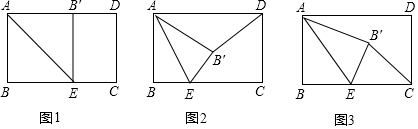
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
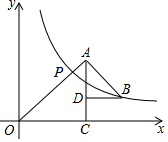 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )| A. | 9 | B. | 6 | C. | 3 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
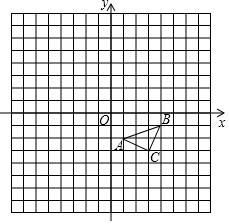 如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).
如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对石家庄市辖区内地下水水质情况的调查 | |
| B. | 对一个社区每天丢弃塑料袋数量的调查 | |
| C. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| D. | 对河北电视台“中华好诗词”栏目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1,其中正确的结论是①②③(把你认为正确结论的序号都填上).
如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1,其中正确的结论是①②③(把你认为正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-x2+9的顶点为A,曲线DE是双曲线y=$\frac{k}{x}$(3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m-3),将抛物线y=-x2+9水平向右移动a个单位,得到抛物线G2.
如图,已知抛物线y=-x2+9的顶点为A,曲线DE是双曲线y=$\frac{k}{x}$(3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m-3),将抛物线y=-x2+9水平向右移动a个单位,得到抛物线G2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com