
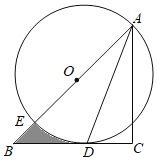
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=![]() ,则图中阴影部分面积为( )
,则图中阴影部分面积为( )
A.4﹣![]() B.2﹣
B.2﹣![]() C.2﹣πD.1﹣
C.2﹣πD.1﹣![]()
【答案】B
【解析】
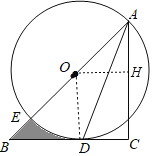
连接OD,OH⊥AC于H,如图,根据切线的性质得到OD⊥BC,则四边形ODCH为矩形,所以OH=CD=![]() ,则OA=
,则OA=![]() OH=2,接着计算出∠BOD=45°,BD=OD=2,然后利用扇形的面积公式,利用图中阴影部分面积=S△OBD﹣S扇形DOE进行计算.
OH=2,接着计算出∠BOD=45°,BD=OD=2,然后利用扇形的面积公式,利用图中阴影部分面积=S△OBD﹣S扇形DOE进行计算.
解:连接OD,过O作OH⊥AC于H,如图,
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵⊙O与BC相切于点D,
∴OD⊥BC,
∴四边形ODCH为矩形,
∴OH=CD=![]() ,
,
在Rt△OAH中,∠OAH=45°,
∴OA=![]() OH=2,
OH=2,
在Rt△OBD中,∵∠B=45°,
∴∠BOD=45°,BD=OD=2,
∴图中阴影部分面积=S△OBD﹣S扇形DOE
=0.5×2×2﹣![]()
=2﹣![]() π.
π.
故选:B.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】为阻断新冠疫情向校园蔓延,确保师生生命安全和身体健康,教育部通知,2020年春季学期延期开学,利用网上平台,停课不停学”,某校对初三全体学生数学线上学习情况进行调查,随机抽取部分学生的4月月诊断性测试成绩,按由高到低分为A,B,C,D四个等级,根据调查的数据绘制成如下的条形统计图和扇形统计图,请根据图中的信息,解答下列问题:
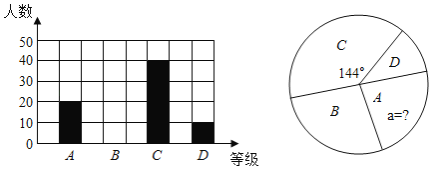
(1)该校共抽查了 名同学的数学测试成绩,扇形统计图中A等级所占的百分比a= ;
(2)补全条形统计图;
(3)若该校初三共有1180名同学,请估计该校初三学生数学测试成绩优秀(测试成绩B级以上为优秀,含B级)约有 名;
(4)该校老师想从两男、两女四位学生中随机选择两位了解平时线上学习情况,请用列表或画树形图的方法求出恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,-3),在抛物线的对称轴上是否存在一点P,使得EP+FP最小,如果存在,求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
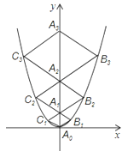
【题目】二次函数y=![]() x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形A2019B2020A2020C2020的周长为________.
x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形A2019B2020A2020C2020的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并解决相应问题:
小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1、b1、c1是常数)与y=a2x2+b2x+c2(a2≠0,a2、b2、c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则这两个函数互为“旋转函数”.求函数y=2x2﹣3x+1的旋转函数,小明是这样思考的,由函数y=2x2﹣3x+1可知,a1=2,b1=﹣3,c1=1,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)写出函数y=x2﹣4x+3的旋转函数.
(2)若函数y=5x2+(m﹣1)x+n与y=﹣5x2﹣nx﹣3互为旋转函数,求(m+n)2020的值.
(3)已知函数y=2(x﹣1)(x+3)的图象与x轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试求证:经过点A1、B1、C1的二次函数与y=2(x﹣1)(x+3)互为“旋转函数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
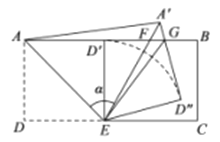
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,把△EAD沿AE折叠,使点D恰好落在AB边上的
,把△EAD沿AE折叠,使点D恰好落在AB边上的![]() 处,再将
处,再将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,得到
,得到![]() ,使得
,使得![]() 恰好经过
恰好经过![]() 的中点F.
的中点F.![]() 交AB于点G,连接
交AB于点G,连接![]() 有如下结论:①
有如下结论:①![]() 的长度是
的长度是![]() ;②弧
;②弧![]() 的长度是
的长度是![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确的序号是________.
.上述结论中,所有正确的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.

(1)若AB=4,求弧CD的长.
(2)若弧BC=弧AD,AD=AP. 求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.

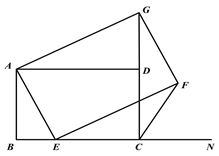
图(1) 图(2)
(1)连接GD,求证:DG=BE;
(2)连接FC,求∠FCN的度数;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=m,BC=n(m、n为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含m、n的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请画图说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com