
分析 首先方程化为[x]=x2-3,根据x-1<[x]≤x得到x-1<x2-3≤x,进一步可得关于x的不等式组,解不等式组即可求得x的值,则代入方程即可求得x的值,注意要检验.
解答 解:方程化为[x]=x2-3,
∵x-1<[x]≤x,
∴x-1<x2-3≤x,
由x-1<x2-3 得 x<-1 或 x>2;
由x2-3≤x 得$\frac{1-\sqrt{13}}{2}$≤x≤$\frac{1+\sqrt{13}}{2}$,由此可得$\frac{1-\sqrt{13}}{2}$≤x<-1或2<x≤$\frac{1+\sqrt{13}}{2}$,
则[x]=-2或2.
①[x]=-2 时,代入方程得x2=3-2=1,
解得:x=±1,与[x]=-2 矛盾;
②[x]=2时,代入方程得x2=3+2=5,
解得x=±$\sqrt{5}$,
结合[x]=2 得 x=$\sqrt{5}$.所以,原方程的解是 x=$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 此题考查了取整函数的知识.注意x-1<[x]≤x性质的应用是解此题的关键,难度较大.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | a=4,b=6,c=5,d=10 | B. | a=2,b=4,c=3,d=6 | ||
| C. | a=2,b=$\sqrt{5}$,c=2$\sqrt{5}$,d=10 | D. | a=0.8,b=3,c=1,d=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
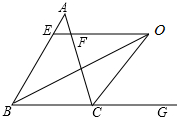 如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.
如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com