
分析 (1)先移项,然后根据提公因式法可以解答此方程;
(2)由题意可知,△≥0,从而可以求得m的取值范围.
解答 解:(1)7x(5x+2)=6(5x+2)
7x(5x+2)-6(5x+2)=0
(5x+2)(7x-6)=0,
∴5x+2=0或7x-6=0,
解得,x1=-$\frac{2}{5}$,x2=$\frac{6}{7}$;
(2)∵于x的一元二次方程x2+3x+m-1=0有两个实数根,
∴32-4×1×(m-1)≥0,
解得,m≤$\frac{13}{4}$,
即m的取值范围是m≤$\frac{13}{4}$.
点评 本题考查解一元二次方程、根的判别式,解题的关键是明确它们各自的意义.


科目:初中数学 来源: 题型:选择题
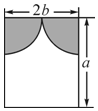 长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )| A. | 2a2-πb2 | B. | 2a2-$\frac{π}{2}$b2 | C. | 2ab-πb2 | D. | 2ab-$\frac{π}{2}$b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
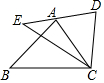 如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( )
如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) ”内,应填×5;第二个运算框“
”内,应填×5;第二个运算框“ ”内,应填-3;
”内,应填-3;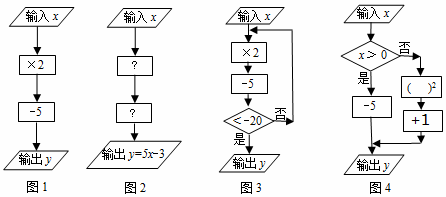
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
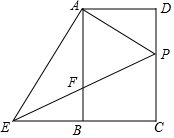 如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.
如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com